Länge einer Seite im Sehnenviereck

Question

Auf einem Halbkreis mit dem Durchmesser \( \overline{|AB|} \)=50 liegen die Punkte C und D. \( \overline{|AD|} \)=30 und \( \overline{|BC|} \)=10·√5. Wie groß ist \( \overline{|DC|} \)?

Comments

f=BD=40

e=AC=20√5

a=50

b=10√5

c=?

d=30

ac+bd=ef

50c+300√5=800√5

50c=500√5

c=DC=10√5

:-)

---

ac+bd=ef

Ist das Ptolemäos?

---

Das weiß ich nicht. Google lieferte mir mit der Suche nach "Sehnenviereck" die passende Formel. Da ich sie nicht hergeleitet habe, habe ich mein Ergebnis als Kommentar gepostet.

https://www.mathetreff-online.de/wissen/mathelexikon/sehnenviereck#:~:text=Da%20der%20Kreis%20durch%20alle,d)%20%3D%20e%20%C2%B7%20f.

---

Ist das Ptolemäos?

Kommentiert vor 1 Stunde von abakus

Das weiß ich nicht.

Dann warst du genau so faul wie ich. Ich hätte auch, meiner Vermutung folgend, ohne dich zu fragen nach diesem Satz googeln können ...

Answer 1

1.) Kreis um \(M(0|0)\) mit \(r=25\):             \(x^2+y^2=625\)

2.) Kreis um \(A(-25|0)\) mit \(r=30\):          \((x+25)^2+y^2=900\) schneidet 1.)  in \(D(-7|24)\)

3.) Kreis um \(B(25|0)\) mit \(r=10*\sqrt{5}\):    \((x-25)^2+y^2=500\) schneidet 1.)  in \(C(15|20)\)

Strecke CD: \( \sqrt{(15+7)^2+(20-24)^2}=\sqrt{22^2+(-4)^2}=\sqrt{484+16}=\sqrt{500}\\=10*\sqrt{5} \)

Comments

(Das ist ein Kommentar!)

Alternative:

Das rechtwinklige Dreieck \(\triangle ABD\) hat die Seitenverhältnisse \(3:4:5\) und kann somit in ein quadratisches Raster mit Abstand \(10\) so eingezeichnet werden, dass die drei Punkte auf den Gitterpunkten liegen.

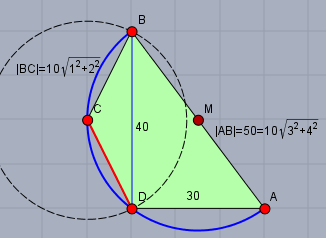
Zeichnet man einen weiteren Punkt \(C^*\) ein, ausgehend von \(B\) nach links um 1 und um 2 Gitterpunkte nach unten (s. Zeichnung), so ist $$|BC^*| = 10 \sqrt{1^2+2^2} = 10\sqrt{5} = |BC|$$Da der Gitterpunkt \(C^*\) vom Mittelpunkt \(M\) den Abstand \(2,5\cdot 10=25 = |A-B|/2\) hat, liegt \(C^*\) auch auf dem Kreis.

Daraus folgt \(C=C^*\). Und aus der Anordung von \(DBC\) im Raster folgt$$|CD| = |BC| = 10\sqrt{5}$$