Sekanten- und Tangenten-Aufgabe

Question

Aufgabe:

Zu einer Sekante gibt es in dem selben Kreis genau eine/ zwei/ keine parallele Tangente. (Antwortmöglichkeiten)

Problem/Ansatz:

Ich verstehe die Aufgabe nicht so wirklich.

Answer 1

Hallo,

Willkommen in der Mathelounge!

schau Dir folgendes Applet an:

https://jsfiddle.net/WernerSalomon/2j90y3ef/7/

und bewege den gelben Punkt \(X\) mit der Maus. So kannst Du jede beliebeige Position einer Tangente (grün) anfahren.

An welchen Positionen verläuft dann die Tangente parallel zur blauen Sekante? Und wieviel Positionen sind das?

Falls doch noch Fragen bleiben, so melde Dich bitte.

Gruß Werner

PS.: mit einem Smartphone geht das wahrscheinlich nicht!

Comments

Mit meinem Smartphone funktioniert es.

:-)

---

Mit meinem Smartphone funktioniert es.

Nokia?

---

Der große Koreaner Samsung.

:-)

Gibt es überhaupt Nokia-Smartphones?

Answer 2

es hilft guck dir dieses Video an.

Answer 3

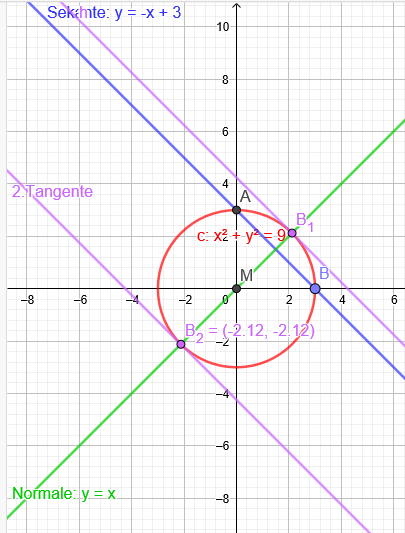
Kreis: x^2+y^2=9

Sekante: y=-x+3    Eine Normale durch den Mittelpunkt des Kreises zu der Sekante schneidet den Kreis in den Berührpunkten der Tangenten.

Normale :y=x  

x²+x²=9

x²=\( \frac{9}{2} \)  |\( \sqrt{} \)

x₁=\( \frac{3}{2} \)*\( \sqrt{2} \)       y₁=\( \frac{3}{2} \)*\( \sqrt{2} \)

x₂=-\( \frac{3}{2} \)*\( \sqrt{2} \)      y₂=-\( \frac{3}{2} \)*\( \sqrt{2} \)

Somit existieren 2 parallele Tangenten.