Wie bestimme ich die Grenzwerte

Question

Hallo, ich versuche die folgenden Grenzwerte zu berechnen und habe für

a) 0

b) komme ich nicht weiter

c) schaffe ich auch nicht

d) 1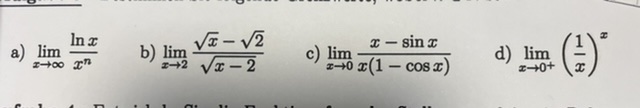

Könnte mir bitte jemand weiterhelfen :)

a) \( \lim \limits_{x \rightarrow \infty} \frac{\ln x}{x^{n}} \)
b) \( \lim \limits_{x \rightarrow 2} \frac{\sqrt{x}-\sqrt{2}}{\sqrt{x-2}} \)
c) \( \lim \limits_{x \rightarrow 0} \frac{x-\sin x}{x(1-\cos x)} \)
d) \( \lim \limits_{x \rightarrow 0^{+}}\left(\frac{1}{x}\right)^{x} \)

Answer 1

b) √x ausklammern und kürzen

c) L'Hospital

d) (1/x)^x = e^(x*ln(1/x))

Comments

b) √x ausklammern und kürzen

Meinst du so \(\dfrac{\sqrt x-\sqrt2}{\sqrt{x-2}}=\dfrac{1-\sqrt{\tfrac2x}}{\sqrt{1-\tfrac2x}}\)  ? Wie geht's dann weiter?

---

Ich hatte jetzt nur das untere x aus der Wurzel unter dem Bruch ausgeklammert und beide Wurzel x gekürzt, aber weiter kam ich jetzt auch nicht mehr

---

L'Hospital klappt auch bei b): \(\displaystyle\lim_{x\to2}\frac{\sqrt x-\sqrt2}{\sqrt{x-2}}=\lim_{x\to2}\frac{\sqrt{x-2}}{\sqrt x}=0\).