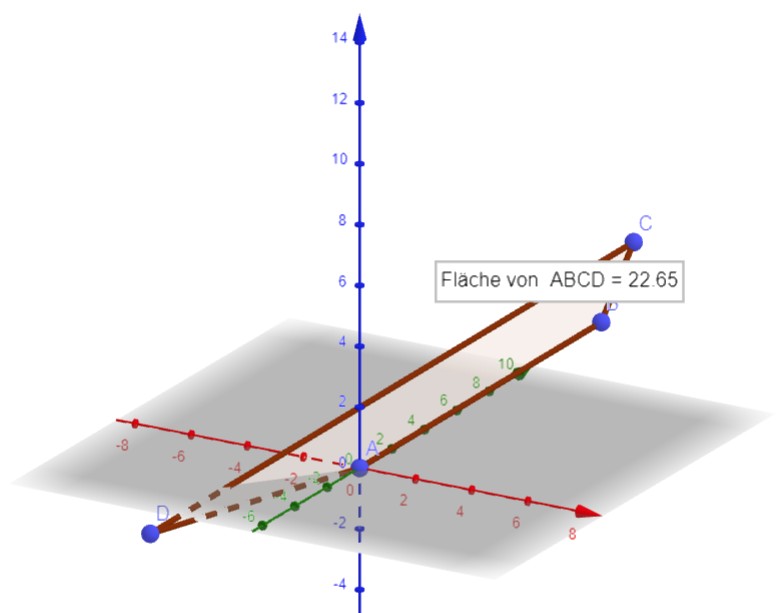
Gegeben sind die Punkte A(0; 0; 0), B(4; 8; 3), C(4; 10; 5), D(−4; −6; −1) und S(3; 2; 3).
AB = [4, 8, 3]
DC = [8, 16, 6]
AD = [-4, -6, -1]
AB und DC sind linear abhängig und damit parallel.
AB und AD sind linear unabhängig.
Damit ist das aufgespannte Viereck ein Trapez.
Flächeninhalt
h = ABS([-4, -6, -1] ⨯ [4, 8, 3])/ABS([4, 8, 3]) = 2/89·√5073
A = 1/2·(ABS([4, 8, 3]) + ABS([8, 16, 6]))·2/89·√5073 = 3·√57 = 22.65 FE
Skizze