Bestimmen Sie die Koordinaten des Punktes B, der auf allen Geraden der Schar liegt.

Question

Aufgabe:

Bestimmen sie die Koordinaten des Punktes B, der auf allen Geraden der Schar liegt.

Funktionenschar: f(x)=mx - 2m + 1

Problem/Ansatz:

Habe eine Aufgabe in dieser Richtung noch nie bearbeitet

Answer 1

Bestimmen sie die Koordinaten des Punktes B, der auf allen Geraden der Schar liegt.  Funktionenschar: f(x)=mx - 2m + 1

f(x)=mx - 2m + 1    und g(x)=(m+1)*x - 2*(m+1)+1=mx+x-2m-2+1

mx - 2m + 1=mx+x-2m-2+1

0=x-2

x=2   f(2)=m*2 - 2m + 1=1

B(2|1)

Answer 2

Hallo,

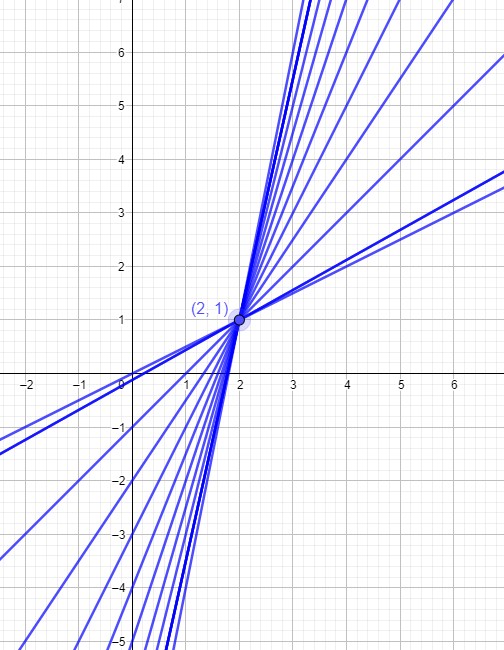
Wenn ein gemeinsamer Schnittpunkt aller Funktionsgraphen einer Schar vorhanden ist, dann muss es eine Stelle x geben, an der der Parameter, hier m, wegfällt.

Forme die Funktionsgleichung um:

\(f_m(x)=mx-2m+1\\ =m\cdot (x-2)+1\)

m fällt weg, wenn x = 2.

f(2)= 2m-2m+1 = 1

Also B (2|1)

Gruß, Silvia

Answer 3

f _m ( x ) = mx - 2m + 1
Ich nehme 2 Funktionen mit unterschiedlichen
Steigungen
f _m1 ( x ) = m1 * x - 2*m1 + 1
f _m2 ( x ) = m2 * x - 2*m2 + 1

Schnittpunkt
m1 * x - 2*m1 + 1 = m2 * x - 2*m2 + 1
m1 * ( x - 2  ) + 1 = m2 * ( x - 2 ) + 1
m1 * ( x - 2  ) = m2 * ( x - 2 )

Die Gleichung ist nur dann richtig falls
x - 2 = 0 ist
x = 2

f ( 2 ) = m * 2 - 2m +1
f ( 2 ) = 2m - 2m +1
f ( 2 ) = 1

P ( 2 | 1 )