Kreis Mittelpunktkoordinaten bestimmen

Question

Aufgabe:

Gegeben Punkt A (-5;1) und B (0;16). Beide Punkte liegen auf einem Kreis mit Mittelpunkt auf der Geraden y=1.

Gesucht sind die Mittelpunktkoordinaten.

Problem/Ansatz:

Leider habe ich keine Idee wie man diese Aufgabe am besten angeht.

Answer 1

Hallo,

Leider habe ich keine Idee wie man diese Aufgabe am besten angeht.

Hast Du schon eine Zeichnung gemacht?

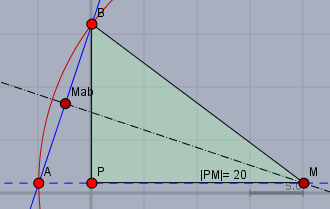
Gesucht ist ein (Mittel-)Punkt \(M\), der von \(B\) genauso weit entfernt ist wie von \(A\). Und seine Y-Koordinate ist ja bereits gegeben. Folglich hat er die Koordinaten \(M(x,1)\). Also ist doch$$(M-A)^2 = (M-B^2)$$ich habe es gleich quadriert, weil die Abstände zwischen zwei Punkten im Koordinatensystem ja über den Pythagoras berechnet werden. Alles einsetzen gibt:$$\begin{aligned}(x-(-5))^2 &= (x-0)^2 + (1-16)^2 \\ x^2+10x+25 &= x^2 + 225\\ 10x&=200\\x&=20\end{aligned}$$Also ist \(M=(20,\,1)\)

Du kannst natürlich auch den Pythagoras für das grüne Dreieck oben im Bild aufstellen ...

Gruß Werner

Answer 2

Gegeben Punkt A (-5|1) und B (0|16).Beide Punkte liegen auf einem Kreis mit Mittelpunkt auf der Geraden y=1. Gesucht sind die Mittelpunktkoordinaten.

Ich habe eine Zeichnung angefertigt. Überlege dir nun die Rechnung dazu.