Steckbriefaufgabe Funktion 4. Grades

Question

Aufgabe:

ganzrationale Funktion 4.Grades:

• Der Graph ist achsensymmetrisch zur y-Achse.

• Die Tangentensteigung in der Nullstelle 2 beträgt 2.

•  −1 ist ein Wendestelle.

Komme leider mit der 2 und 3 Bedingung nicht zurecht. Bekannt ist mir, dass die Funktion wie folgt schonmal aussehen muss= ax^4+cx^2+e

Answer 1

f(x) = ax^4+cx^2+e  ✓

Die Tangentensteigung in der Nullstelle 2    ==> f(2)=0

beträgt 2.  ==>   f ' (2) = 2 

•  −1 ist ein Wendestelle.  ==>   f ' ' (-1) = 0 

Comments

Was kommt dann letztendlich als Gleichung heraus? 1/4x^4-3/2 x^2 +2?

---

Passt astrein !

Answer 2

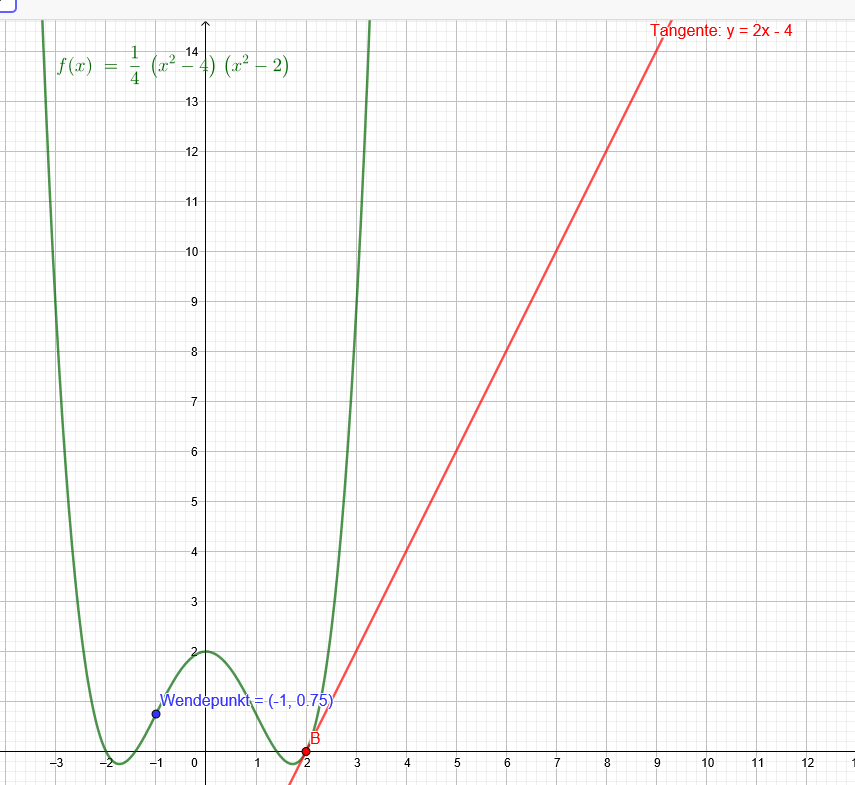
ganzrationale Funktion 4.Grades:

• Der Graph ist achsensymmetrisch zur y-Achse.

• Die Tangentensteigung in der Nullstelle 2 beträgt 2.

•  −1 ist ein Wendestelle.

Weg über die Nullstellenform der Parabel 4.Grades:

f(x)=a*(x+2)*(x-2)*(x+N)*(x-N)=a*[(x^2-4)*(x^2-N^2)]

f´(x)=a*[2x*(x^2-N^2)+(x^2-4)*2x]

f´(2)=a*[2*2*(4-N^2)]=a*[4*(4-N^2)]

1.) a*[4*(4-N^2)]=2

f´´(x)=a*[2*(x^2-N^2)+2x*2x+2x*2x+(x^2-4)*2]

f´´(-1)=a*[2*((-1)^2-N^2)+2*(-1)*2*(-1)+2*(-1)*2*(-1)+((-1)^2-4)*2]=a*[4-2N^2]

2.) a*[4-2N^2]=0

4-2N^2=0

N₁=\( \sqrt{2} \)

N₂=-\( \sqrt{2} \)

1.) a*[4*(4-2)]=2

a=\( \frac{1}{4} \)

f(x)=\( \frac{1}{4} \)*[(x^2-4)*(x^2-2)]