Bestimme die Nullstellen und Extremstellen Nst.: der Funktion f mit f(x)=-2 x^{3}+4 x^{2} .

Question

Aufgabe:

5. Bestimme die Nullstellen und Extremstellen der Funktion f mit \( f(x)=-2 x^{3}+4 x^{2} \).

Problem/Ansatz:

Die Nullstellen der Funktion sind x= 0 und x= 2

Die Extremstellen der Funktion sind ein lokales Minimum bei x= 0 und ein lokales Maximum bei x= \( \frac{3}{4} \).

Answer 1

a) -2x^3+4x^2 = 0

-2x^2(x-2) = 0

x= 0 v x = 2

b)

1. Ableitung Null setzen:

-6x^2+8x = 0

-x(6x-8) = 0

x= 0 v x= 8/6 = 4/3

Comments

Also sind die Lösungen richtig?

---

x= 2 ist falsch.

Nach Min und Max. ist nicht gefragt.

Ich habe es daher nicht geprüft mit der 2. Ableitung.

---

ah, das habe ich übersehen, danke

---

Nee, \(x=2\) ist richtig.

ggT22 hat falsch ausgeklammert:\(\quad-2x^3+4x^2=-2x^2(x\pink-2)\)

---

Also ist die Antwort von Moliets richtig?

---

Ja, Moliets hat alles richtig berechnet.

---

Gibt es eine Möglichkeit die "Beste Antwort" zu wechseln?

---

Ich habe es korrigiert. Sorry, eine Unachtsamkeit.

Bei b) stimmts wieder.

Answer 2

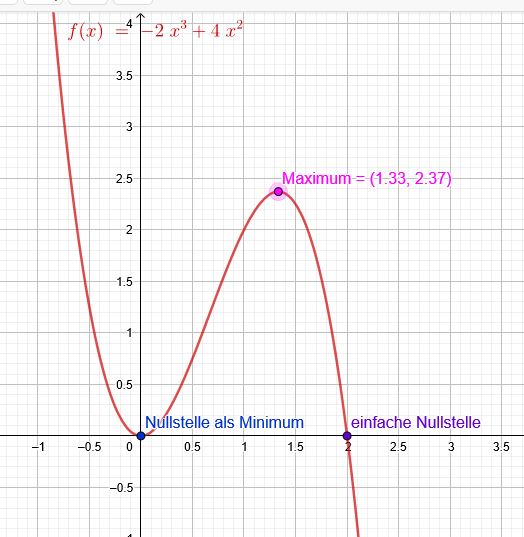
\( f(x)=-2 x^{3}+4 x^{2} \)

Nullstellen:

\(-2 x^{3}+4 x^{2}=0 \)   →   \(- x^{3}+2x^{2}=0 \)   →   \( x^{3}-2x^{2}=0 \)

Satz vom Nullprodukt:

\( x^{2}*(x-2)=0 \)

\(x=0\) doppelte Nullstelle  → Extremwert

\(x=2\)  einfache Nullstelle.

Extremwerte:

\( f´(x)=-6 x^{2}+8 x \)

\( -6 x^{2}+8 x=0 \)   →\( 3 x^{2}-4 x=0 \)

Satz vom Nullprodukt:

\(x_1=0\)   \( f(0)=0 \) siehe oben

\(x_2=\frac{4}{3}\)  \( f(\frac{4}{3})=... \)

Art des Extremwertes:

\( f´´(x)=-12 x+8  \)

\( f´´(0)=8 >0  \) Minimum

\( f´´(\frac{4}{3})=-12 *(\frac{4}{3})+8=-8<0  \)Maximum