Hallo Lena,
Willkommen in der Mathelounge!
Die grundsätzliche Vorgehensweise besteht darin, die Geraden durch die Ecken der Daches des Carports in Richtung des Lichteinfalls zu berechnen.
So wie ich es oben im Bild dargestellt habe, liegt die vordere linke Ecke \(G\) des Carports bei der Koordinate$$G =\begin{pmatrix}5\\ 2.4\\ 2.4\end{pmatrix}$$Die zugehörige Gerade, die an \(G\) vorbei läuft, hätte dann bei niedrigem Stand der Sonne die Gleichung$$l_g:\quad \vec x = \begin{pmatrix}5\\ 2.4\\ 2.4\end{pmatrix} + t\begin{pmatrix}2\\ 3\\ -2\end{pmatrix}$$Der Schatten auf dem Boden hat immer die \(x_3\)-Koordinate \(x_3=0\). Daraus folgt dann (3. Koordinatengleichung)$$x_3=0 = 2,4-2t \implies t =1,2$$D.h. die Position der Ecke \(G'\) des Schattens, die durch \(G\) verursacht wird, liegt bei$$G'= \vec x(t=1,2) = \begin{pmatrix}5\\ 2.4\\ 2.4\end{pmatrix} + 1,2\cdot \begin{pmatrix}2\\ 3\\ -2\end{pmatrix} = \begin{pmatrix}7.4\\ 6\\ 0\end{pmatrix}$$Mache Dir selber eine Skizze, am besten im Grundriss, also von oben, und überlege, welche Ecken des Carports Schatten werfen. Am Ende musst Du dann nur noch die Punkte verbinden.
Zur Berechnung der Schattenfläche habe ich Dir die Schattenfläche für den niedrigen Sonnenstand im Grundriss aufgezeichnet:
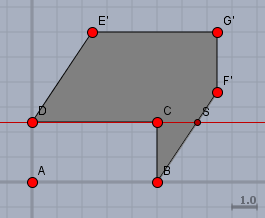
Im Bild geht die \(x_1\)-Achse nach rechts und die \(x_2\)-Achse nach oben. Die Grundstücksgrenze ist die rote Gerade. Alles oberhalb der roten Geraden gehört zum Nachbarn. Folglich ist die Schattenfläche auf dem Nachbargrundstück das 5-Eck \(DSF'G'E'\). Der Punkt \(S\) muss noch zusätzlich berechnet werden.
Die Fläche kann man vielleicht am einfachsten berechnen, wenn man das umhüllende Rechteck bestimmt und dann die beiden überstehenden Dreiecke bei \(SF'\) und \(DE'\) davon abzieht. (zur Kontrolle: 21,84m2)
Falls Du noch Fragen hast, so melde Dich bitte.
Gruß Werner