Aufgabe:
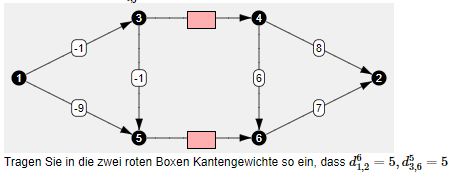
Text erkannt:
Tragen Sie in die zwei roten Boxen Kantengewichte so ein, dass \( d_{1,2}^{6}=5, d_{3,6}^{5}=5 \)
\( d_{i, j}^{0}:=\left\{\begin{array}{ll}0 & i=j \\ l(i, j) & i \neq j,(i, j) \in A \\ \infty & i \neq j,(i, j) \notin A\end{array}\right. \)
\( d_{i, j}^{k}:=\min \left\{d_{i, j}^{k-1}, d_{i, k}^{k-1}+d_{k, j}^{k-1}\right\} \) (hoch k bedeutet, dass nur Knoten aus der Menge {1,...,k} verwendet werden dürfen auf dem Weg von i zu j)
Problem/Ansatz:
Ich habe folgende Schritte bereits berechnet, wobei ich die obere Box als x und die untere Box als y definiert habe
\(d^0_{1,2} = d^1_{1,2} = d^2_{1,2} = d^3_{1,2} = \infty \)
\(d^4_{1,2} = x+7 \)
\(d^5_{1,2} = x+7 \)
\(d^6_{1,2} = ? \) komme hier nicht weiter, weil dieser Ausdruck x und y mehrfach verwendet
und
\(d^0_{3,6} = d^1_{3,6} = d^2_{3,6} = d^3_{3,6} = \infty \)
\(d^4_{3,6} = x+6 \)
\(d^5_{1,2} = min \{x+6, y-1 \} \)
Nach dem letzten Schritt wollte ich die Gleichung gleich 5 setzten und nach den gesuchten Variablen x und y umformen, aber da die Variablen mehrfach auftauchen und nicht bekannt sind, weiß ich nicht welchen Ausdruck ich gleich 5 setzen soll.Ich stehe echt auf dem Schlauch