Welcher Punkt liegt auf welcher Geraden?

Question

Text erkannt:

3 Welcher Punkt liegt auf welcher Geraden?
\begin{tabular}{|c|}
\hline\( P(-1 \mid-9) \) \\
\hline\( P(6,5 \mid 1,5) \) \\
\hline\( P(-10 \mid 0) \) \\
\hline\( P(2,5 \mid-4) \) \\
\( g_{2}: y=-2 x+1 \) \\
\( g_{3}: y=3 x-6 \) \\
\( g_{4}: y=-\frac{2}{5} x-4 \)
\end{tabular}
Zeichen Sie Geraden und Punkte in ein Koordinatensystem. Überprüfen Sie Ihre Ergebnisse. Suchen Sie vier weiteren Punkte, die auf den Geraden \( g_{1} \) bis \( g_{4} \) liegen. Lassen Sie Ihre Nachbarin oder Ihren Nachbarn die Punktprobe durchführen.

Problem/Ansatz:

Wie zeichne ich in einem Koordinatensystem Geraden und Punkte?

Könntet ihr mir bitte ein Beispiel zeigen? :)

Answer 1

Hallo,

die waagerechte ist die x-Achse, die senkrechte die y-Achse.

Links vom Ursprung liegen negative x-Werte, rechts davon positive.

Oberhalb des Ursprungs liegen positive x-Werte, unterhalb negative.

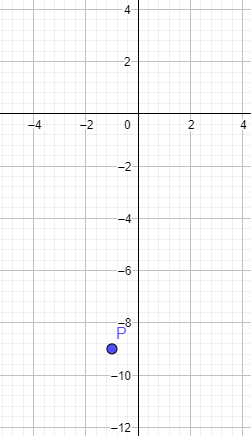
P(-1|9) - Gehe vom Ursprung eine Einheit nach links und 9 nach unten.

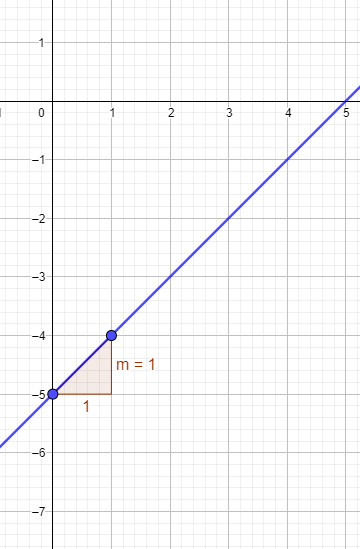
y = x - 5

Allgemeine Form der Geradengleichung y = mx + b

m = Steigung, hier = 1

b = Schnittpunkt mit der y-Achse, hier = -5

Zeichne den Schnittpunkt mit der y-Achse ein, gehe von dort aus eine Einheit nach rechts und eine nach oben. Eine nach oben weil m = +1

 

Für y = -2x + 1 zeichnest du wieder den Schnittpunkt mit der y-Achse bei 1, gehst von dort eine Einheit nach rechts und 2 nach unten, da die Steigung -2 ist.

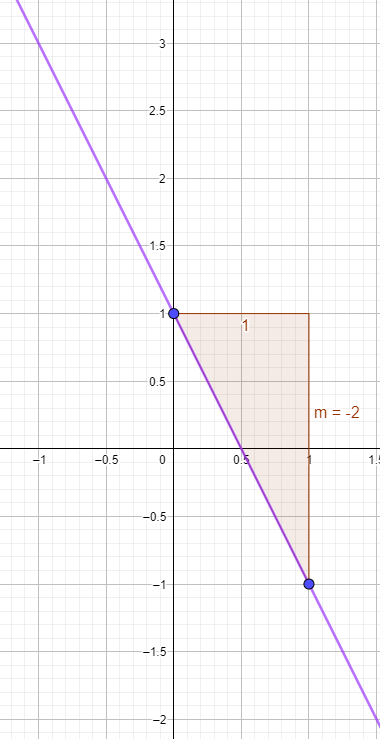
Die beiden Punkte sind natürlich miteinander zu verbinden.

Um rechnerisch herauszufinden, ob ein Punkt auf einer Geraden liegt, kannst du seine Koordinaten in die Gleichung einsetzen.

z.B. P(-1|-9) und y = x-5

-9 = -1-5

9 = -6

Falsche Aussage, also liegt der Punkt nicht auf der Geraden

Gruß, Silvia

Comments

Vielen dank. :)