Veränderung der optimalen Lösung - Lineare Programmierung

Question

Aufgabe:

Text erkannt:

Gegeben sei das Lineare Programm zur Bestimmung eines gewinnmaximierenden Produktionsprogramms bei zwei Produkten \( (1 ; 2) \) und drei Kapazitäten (I;II;III):
\( G=10 x_{1}+5 x_{2} \rightarrow \max ! \)
unter den Nebenbedingunge

Text erkannt:

Kapazität I: \( \quad 5 x_{1}+3 x_{2} \leq 27 \)
Kapazität II: \( \quad 2 x_{1}+x_{2} \leq 10 \)
Kapazität III: \( \quad x_{1}+x_{2} \leq 7 \)
\( x_{1}, x_{2} \geq 0 \)
a) Man berechne die optimale Lösung mithilfe der Simplexmethode.
b) Das Tableau weist eine Besonderheit auf. Man beschreibe kurz, woran man diese Besonderheit erkennt und bestimme die optimale Lösungsmenge.
c) Treten noch weitere Sonderfälle auf? Wenn ja, schildere man, welcher Art sie sind und wie sie festgestellt werden können.
d) Sind die Kapazitäten I und II voll ausgelastet (Begründung!)?
e) Man überlege, wie sich die optimale Lösung verändert, wenn
e \( _{1)} \) Kapazität I um 1 Einheit erhöht werden kann;
e \( _{2)} \) Kapazität II um 1 Einheit erhöht werden kann.

Problem/Ansatz:

Lösung zu b)

Text erkannt:

\(\begin{array}{cccccc|c}  {x}_{1}  &  {x}_{2} &  {y}_{1}  & {y}_{2} &  {y}_{3} & {G} & \\ 0 & 1 & 2 &  -5  & 0 & 0 & 4 \\1 & 0 &  -1 & 3 & 0 & 0 & 3 \\0 & 0 &  -1 & 2 & 1 & 0 & 0 \\ 0 & 0 & 0 & 5 & 0 & 1 & 50 \end{array}\)
\( \underline{x}=\lambda \underline{x}_{1}^{o p t}+(1-\lambda) \underline{x}_{2}^{o p t}=\lambda \cdot\left(\begin{array}{l} 5 \\ 0 \\ 2 \\ 0 \\ 2 \end{array}\right)+(1-\lambda) \cdot\left(\begin{array}{l} 3 \\ 4 \\ 0 \\ 0 \\ 0 \end{array}\right), \quad(0 \leq \lambda \leq 1) \)

Mein Problem hier ist, dass ich nicht weiß, wie ich e) berechne.

Die Kapazitäten I und II sind voll ausgelastet, aber das ist ja eher irrelevant für die Veränderung der optimalen Lösung.

In den Lösungen kommt folgendes raus:

Text erkannt:

e) e \( _{1} \) ) \( x_{1}^{*}=2 ; x_{2}^{*}=6 ; G^{*}=50 \)
\( \left.\mathrm{e}_{2}\right) \quad x_{1}^{*}=6 ; \quad x_{2}^{*}=-1[\Rightarrow \) nicht sinnvoll \( !] ; \mathrm{G}^{*}=55 \)

Ich komme aber nie auf das gleiche Ergebnis.

Wie erhält man das Richtige?

Answer 1

Die Kapazitäten bei

\(\small Tableau \, :=  \, \left\{ \left(\begin{array}{rrrrr}5&3&1&0&0\\2&1&0&1&0\\1&1&0&0&1\\\end{array}\right), \left(\begin{array}{r}3\\4\\0\\0\\0\\\end{array}\right), \left(\begin{array}{r}27\\10\\7\\\end{array}\right), 50 \right\} \)

sind voll ausgelastet.

Die Besonderheit ist, das die Gewinngerade die gleiche Steigung wie Kapazität II hat. Auch gut zu sehen in grafischen Lösung

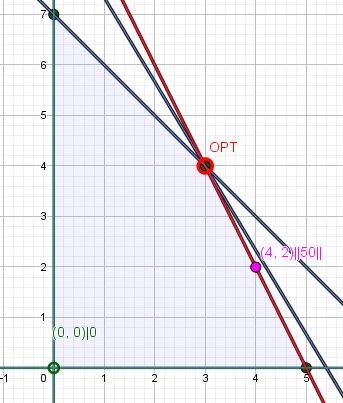
dort bleiben auch noch Kapazitäten - Alle Punkte auf der Geraden von Opt (3,4) bis (5,0) liefern das Maximum.

\(\small Tableau \, :=  \, \left\{ \left(\begin{array}{rrrrr}5&3&1&0&0\\2&1&0&1&0\\1&1&0&0&1\\\end{array}\right), \left(\begin{array}{r}4\\2\\1\\1\\1\\\end{array}\right), \left(\begin{array}{r}27\\11\\7\\\end{array}\right), 50 \right\} \)

Was bei c) eine Lösung sein soll, verstehe ich nicht

\(\small Tableau \, :=  \, \left\{ \left(\begin{array}{rrrrr}5&3&1&0&0\\2&1&0&1&0\\1&1&0&0&1\\\end{array}\right), \left(\begin{array}{r}2\\6\\-1\\1\\-1\\\end{array}\right), \left(\begin{array}{r}27\\11\\7\\\end{array}\right), 50 \right\} \)

2 Kapazitäten werden überschritten.

und wenn man II erhöht finde ich

\(\small Tableau \, :=  \, \left\{ \left(\begin{array}{rrrrr}5&3&1&0&0\\2&1&0&1&0\\1&1&0&0&1\\\end{array}\right), \left(\begin{array}{r}5.4\\0\\0\\0.2\\1.6\\\end{array}\right), \left(\begin{array}{r}27\\11\\7\\\end{array}\right), 54 \right\} \)