Nebenbedingungen für Simplex-Tableau, mit Ansatz

Question

Hallo, ich habe die folgende Aufgabe, aber komme einfach nicht auf das Ergebnis.

Die Aufgabe lautet: Ein Betrieb möchte 1000 m² Nutzfläche seines Landes gewinnmaximal mit Blumen und Gemüse bepflanzen. Hierfür möchte der Betrieb insgesamt 7200 Euro einsetzen. Für den Anbau sind Arbeits- und Materialkosten von 6 Euro pro m² für Gemüse und 9 Euro pro m² für Blumen zu veranschlagen. Der zu erwartende Stückdeckungsbeitrag aus dem Anbau beträgt 10 Euro pro m² für Gemüse und 20 Euro pro m² für Blumen. Fixe Kosten sind in Höhe von 2000 Euro zu berücksichtigen. Aufgrund von Schatten sind nur insgesamt 600 m² für den Blumenanbau geeignet.

Damit muss ich ein lineares Optimierungsmodell formulieren und mit dem Simplex-Algorithmus lösen. Jedoch habe ich Schwierigkeiten, die Nebenbedingungen aufzustellen, und das mit dem Stückdeckungsbeitrag verwirrt mich. (x₁ = Anbaufläche für Gemüse in m², x₂ = Anbaufläche für Blumen in m²)

Meine Ansätze:

max z = 10⋅x₁ + 20⋅x₂

u.d.N. x₁ + x₂ ≤ 1000

x₂ ≤ 600

6⋅x₁ + 9⋅x₂ + 2000 ≤ 7200

x₁,x₂ ≥ 0

Den Simplex-Algorithmus zu lösen wäre kein Problem, aber meine Nebenbedingungen sind falsch oder auch die Funktion selbst. Kann mir hierbei jemand behilflich sein? :-)

Answer 1

Ich halte Dein LP für richtig.

Vielleicht stimmt die Lösung nicht. Was hast Du für ein Optimum?

Comments

in der Lösung ist das zweite Tableau angegeben. Demnach ist x2 die niedrigste Zahl, sodass meine Funktion bereits falsch sein müsste

Weißt du, ob der Stückdeckungsbeitrag einfach den Gewinn angibt? Dh Stückdeckungsbeitrag mal die Menge

---

ist das zweite Tableau angegeben. Demnach ist x₂ die niedrigste Zahl

Wie Du meinen? Ich verstehe die beiden Sätze nicht.

ob der Stückdeckungsbeitrag einfach den Gewinn angibt?

Stückdeckungsbeitrag mal Menge gibt nicht Gewinn, sondern Deckungsbeitrag.

Darum nochmals, auf was für ein Optimum kommst Du?

---

Ich komme auf z=15000 x1=300; x2=600

Aber kann das denn dann die Zielfunktion sein, wenn z = 10⋅x1 + 20⋅x2 die Stückdeckungsbeiträge angibt?

---

Dein Optimum ist darum falsch, weil man dann inkl. Fixkosten 9200 ausgibt anstatt 7200. Die dritte Nebenbedingung ist verletzt.

Bei maximalem DB ist auch der Gewinn maximal. Denn die Fixkosten sind konstant, darum heißen sie so.

---

Vielen Dank! Könntest du mir dann bei der dritten NB behilflich sein?

Wenn ich bei der dritten NB die Fixkosten von 2000 auf die andere Seite bringe, sind es doch 5200 und nicht 7200. Oder denke ich da falsch?

---

Bzw. wo muss ich die Fixkosten einbinden, in welche Nebenbedingung?

---

Deine dritte Nebenbedingung ist ja gut so, wie Du sie aufgeschrieben hast.

Answer 2

Schaun mer erstmal in die Grafik

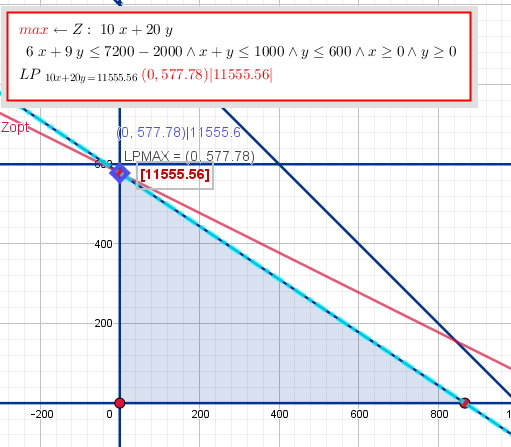
Das ergibt ein Start-Tableau von

\(\small \left(\begin{array}{rrrrrr}6&9&1&0&0&5200\\1&1&0&1&0&1000\\0&1&0&0&1&600\\-10&-20&0&0&0&0\\\end{array}\right)\)

und dann

\(\small \left(\begin{array}{rrrrrr}0.667&1&0.111&0&0&\textcolor{red}{577.778}\\0.333&0&-0.111&1&0&422.222\\-0.667&0&-0.111&0&1&22.222\\3.333&0&2.222&0&0&\textcolor{red}{11555.556}\\\end{array}\right) \)

also kein Gemüse heute....

Comments

Das stimmt leider nicht, habe nun die Lösung vor mir und die Zielfunktion ist eine ganz andere. Gewinn= 7800, Gemüse x1= 300 und Blumen x2= 600

---

Siehe dazu meinen Hinweis weiter oben:

Dein Optimum ist darum falsch, weil man dann inkl. Fixkosten 9200 ausgibt anstatt 7200. Die dritte Nebenbedingung ist verletzt.

---

Meine Rechnung arbeitet mit Deinen Daten und ist stimmig - wo kommt plötzlich ein Gewinnbetrag von 7800  her - welcher Gewinn - davon steht nix in Deiner Aufgabe.

(300,600) ist eine Lösung ohne Berücksichtigung der Fixkosten!

originaltext?