Trigonometrie; Um wie viel Grad steht die Sonne über dem Horizont?

Question

Der Mast eines Segelbootes wirft einen waagerechten Schatten, dessen Länge vom Stand der Sonne abhängt. Um wie viel Grad steht die Sonne über dem Horizont, wenn der Schatten 

a) genauso lang

b) halb so lang

c) dreimal so lang

ist wie der Mast?

 

Meine Skizze s.o. Diese wird wohl richtig sein!

a) tan (α) = m / s.

Wenn s = m, dann müsste α = 45° sein. Das kann ich nachvollziehen.

b) s = m / 2 (?),  und genau hier komme ich nicht weiter.

c) s = 3m (???)

 

Bitte, wenn mir das jemand nachvollziehbar erklären könnte, das wäre schön!

Dankeschön und liebe Grüße,

Sophie

Answer 1

Hi Sophie :-)

 

so sieht die Aufgabe in einer erweiterten Skizze aus:

Rote Gerade, der Schatten ist genauso lang wie der Mast:

tan(α) = Gegenkathete/Ankathete = 1/1

α = arctan(1) = 45°

 

Blaue Gerade, der Schatten ist doppelt so lang wie der Mast:

tan(α) = Gegenkathete/Ankathete = 1/2

α = arctan(1/2) ≈ 26,6°

 

Grüne Gerade, der Schatten ist dreimal so lang wie der Mast:

tan(α) = Gegenkathete/Ankathete = 1/3

α = arctan(1/3) ≈ 18,4°

 

Liebe Grüße

Andreas

Comments

Oh sorry, habe b) falsch gelesen:
Also

tan(α) = Gegenkathete/Ankathete = 1/(1/2) = 2

α = arctan(2) ≈ 63,4°

---

Andreas,

dankeschön für Deine Hilfe, aber ich verstehe Deine Rechnung leider nicht. Habe ich vielleicht gerade für heute wieder meinen Zenit überschritten oder warum geht es nicht in meinen Kopf, "was" Du durch "was" teilst?

Liebe Grüße,

Sophie

---

Nun mal sehen Sophie,

vielleicht wird es so klarer:

 

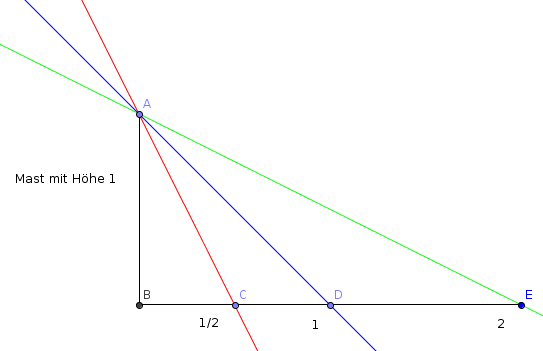
Wir haben doch in allen Teilaufgaben ein rechtwinkliges Dreieck gegeben.

Der Mast (Gegenkathete) wird repräsentiert durch die Strecke AB in obiger Skizze, die Hypotenusen sind

AC bzw. AD bzw. AE.

Nochmals eine kleine Skizze, damit wir nicht so viel scrollen müssen:

Tangens = Gegenkathete/Ankathete

Für den Winkel α, den wir am Punkt C (rot) oder D (blau) oder E (grün) ansetzen, ist die Gegenkathete jeweils der Mast mit der (Standard-)Höhe 1. Die Ankathete ist jeweils die Strecke auf der x-Achse bis zum entsprechenden Punkt.

Also hätten wir für

C (rot):       Tangens = 1/(1/2)

D (blau):    Tangens = 1/1

E (grün):    Tangens = 1/2

 

Der Rest verläuft nach Schema F: arctan der Werte (2 bzw. 1 bzw. 0,5) ergibt α.

 

Etwas deutlicher geworden?

 

Liebe Grüße

Andreas

---

Vergiss bitte meinen obigen Kommentar!
Die Rechnung ist ja ganz simpel und selbstverständlich nachvollziehbar.....

Also ganz lieben Dank an Dich!

Sophie

P.S. Danke Dir auch für "Du weißt schon". Ich habe mich ehrlich gefreut!

---

Immer wieder gern, egal, welches Medium oder Thema :-D