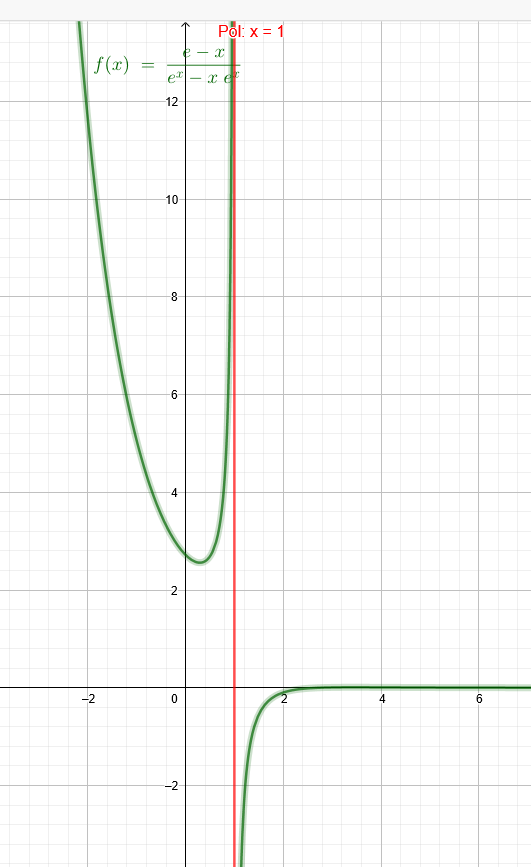
e)\( f(x)=\frac{e-x}{e^{x}-x e^{x}} \)=\( \frac{e-x}{e^x*(1-x)} \)
Polstelle: Nenner =0
\( e^{x} \)*(1-x)=0 \( e^{x} \)≠0 x=1
Verhalten bei Annäherung an die Definitionslücken:
\( f(x)=\frac{e-x}{e^{x}-x \cdot e^{x}} \)
\( f(1,2)=\frac{e-1,2}{e^{1,2}-1,2 \cdot e^{1,2}} \approx-2,28 \)
\( f(1,1)=\frac{e-1,1}{e^{1,1}-1,1 \cdot e^{1,1}} \approx-5,38 \)
\( f(1,01)=\frac{e-1,01}{e^{1,01}-1,01 \cdot e^{1,01}} \approx-62,21 \)
Es läuft gegen \( -\infty \)
\( f(x)=\frac{e-x}{e^{x}-x \cdot e^{x}} \)
\( f(0,9)=\frac{e-0,9}{e^{0,9}-0,9 \cdot e^{0,9}} \approx 7,39 \)
\( f(0,99)=\frac{e-0,99}{e^{0,99}-0,99 \cdot e^{0,99}} \approx 64,21 \)
Es läuft gegen \( +\infty \)