Aufgabe:
es soll die Fläche berechnet werden, die durch die Schnittpunkte dreier Einzelfunktionen entsteht
Problem/Ansatz:
Die Fläche "A" soll berechnet werden, ist dies mit konventionellen Methoden möglich, oder müssen da beliebige Teilflächen gebildet werden, oder ist dies gar nicht möglich (bisher)?
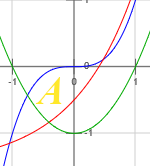
Funktionen: x^2-1, e^x-b, x^3, b weiß ich nicht mehr...,könnte ich bei x^3=x^2-1 und e^x-b=x^2-1 eine erste Teilfläche ermitteln?
Danke für die Antworten! Viele Grüße, Bert Wichmann!