Aufgabe:
Vektoren als Linearkombination schreiben
Problem/Ansatz:
Text erkannt:
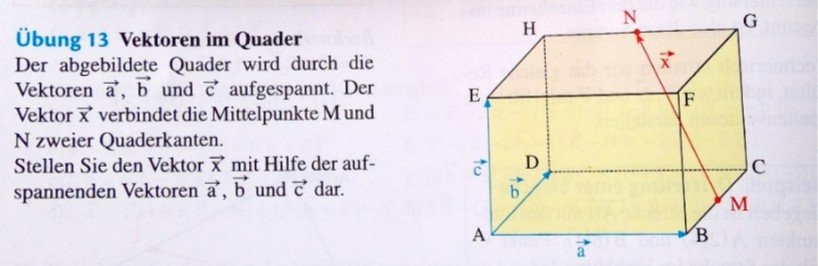
Übung 13 Vektoren im Quader Der abgebildete Quader wird durch die Vektoren \( \vec{a}, \vec{b} \) und \( \vec{c} \) aufgespannt. Der Vektoren \( \vec{a}, \vec{b} \) und \( \vec{c} \) aufgespannt. Der Vektor \( \vec{x} \) verbindet die Mittelpunkte M und Ne zweier Quaderkanten. Stellen Sie den Vektor \( \vec{x} \) mit Hilfe der aufspannenden Vektoren \( \vec{a}, \vec{b} \) und \( \vec{c} \) dar.
Die Lösung im Buch zu dieser Aufgabe ist folgende:
x=> = 1/2b=> + c=> - 1/2a=>
Für mich macht dies aber absolut keinen Sinn, vielleicht habe ich aber auch einen Denkfehler. Ich denke mir:
Durch das 1/2b=> bewege ich mich auf der X-Achse um die Hälfte von b nach vorne. Durch den Vektor c=> bewege ich mich nun auf der Z-Achse um den Vektor c nach oben . Ich befinde mich nun also schon auf der Höhe vom zielführenden Vektor x=>, jedoch stimmen die Plätze auf X und Y Achse noch nicht. Würde ich nun -1/2a=> an den vorherigen Vektor anhängen, so wäre das doch gar nicht mehr möglich, weil ich über den Quader hinaus nach links zeichnen müsste und das ganze keinen Sinn ergibt.
Für mich wäre logisch: x=> = b=> + 1/2a=> + c=>
Ist die Lösung falsch oder habe ich einen Denkfehler?