Trigonometrie - Berechne Alpha

Question

Text erkannt:

RaOIUS \( r=\overline{B M}=5, \overline{A O}=8 \) Beascmne d

Comments

Hallo,

ich rate mal, dass das \(\overline{A{\color{red}D}}=8\) heißen soll - oder?

Ist das eine Wettbewerbsaufgabe?

---

Ja, Entschuldigung, dass meine Schrift nicht ganz leserlich ist. Genau, die Strecke AD beträgt 8. Die Aufgabe gehört zu einem Schülern, und ich kann sie einfach nicht lösen.

Answer 1

Hallo,

Die Winkel \(\angle DAB\) und \(\angle DCA\) (gelb) sind gleich groß (Umfangswinkel über der Strecke \(BD\)). Die Dreiecke \(\triangle BAM\) (grün) und \(\triangle ADM\) (blau) sind beide gleichschenklig. Bei \(\triangle BAM\) ist folglich \(\alpha = \angle MAB\) (blau).

Wenn \(2\alpha = 2\angle MAB = \angle DAB\) sein soll, muss \(\angle DAM = \alpha\) sein. Daraus folgt, dass die beiden Dreiecke \(\triangle BAM\) und \(\triangle ADM\) beide den Basiswinkel \(\alpha\) haben und daher gleich sind.$$\implies |AB| = |AD| \implies \alpha = \arccos\left(\frac{\frac12|AB|}{|BM|}\right) = \arccos(0,8) \approx 36,9°$$Gruß Werner

Comments

Wunderbar! Vielen Dank für deine Lösung. Leider habe ich vorher nicht bemerkt, dass die Winkel DAB und DCA gleich sind.

Answer 2

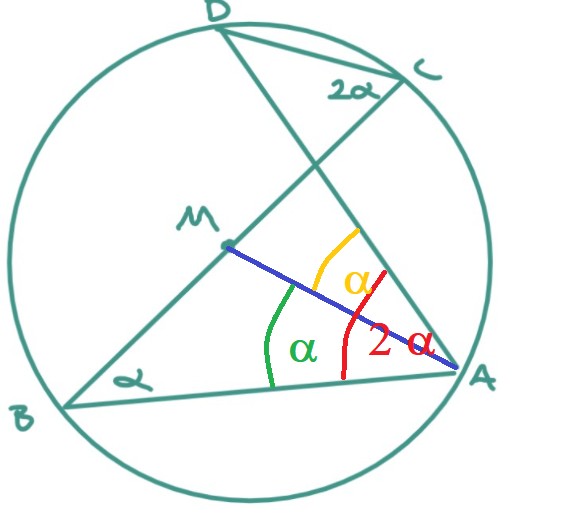
1) Der rote Winkel ist (auch) 2α. Warum?

2) Der grüne Winkel ist (auch) α. Warum?

3) Wegen 1) und 2) ist der orange Winkel auch α.

4) Dieser orange Winkel α ist Innenwinkel im Dreieck ADM, dessen Seitenlängen alle bekannt sind.

Damit ist die Berechnung dieses Innenwinkels α mit dem Kosinussatz oder im halbierten Dreieck möglich.

Comments

∠ADC = α (Peripheriewinkelsatz)  ⇒ ∠BDA = 90°-α (Thales)

∠CBD = 90°-2α (Thales)  ⇒ ∠ABD = 90°-α

⇒ BA = AD

α mit Kosinus im rechtw. Δ BAC

---

Das ist auch schön.