Vektorrechnung - Beweis, dass sie sich halbieren

Question

Hallo! Folgende Aufgabenstellung ist gegeben:

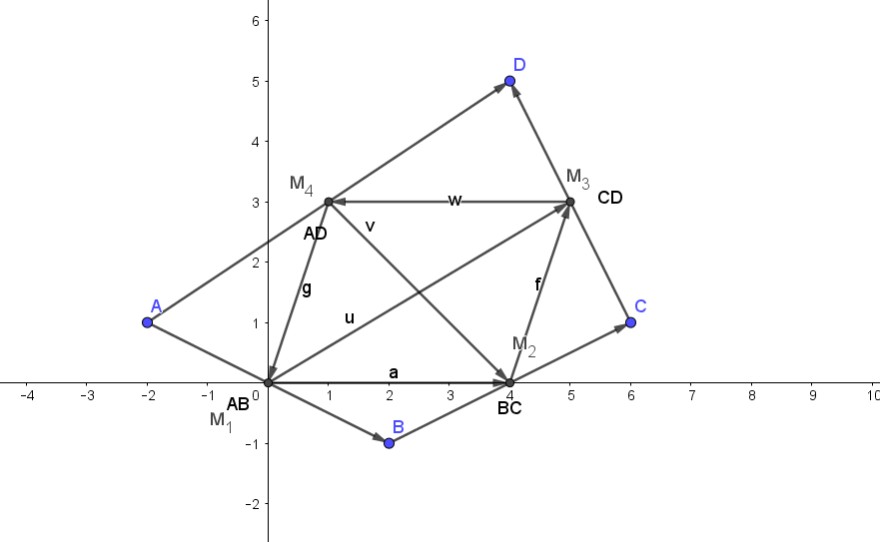
a) Von einem Viereck ABCD werden die gegenüberliegenden Seitenmittelpunkte M_1 und M_3 bzw M_2 und M_4 miteinander verbunden. Zeige rechnerisch, dass sich diese Verbindungslinien gegenseitig halbieren.

b) Zeige rechnerisch, dass es sich beim Viereck M_1, M_2, M_3, M_4 um ein Parallelogramm handelt.

A(-2, 1), B (2,-1), C (6, 1), D (4, 5)

Berechnet habe ich folgendes:

AB = (4, -2), BC = (4, 2), CD = (-2, 4), AD = (6, 4)

M_1 = (0,0), M_2 = (4,0), M_3 = (5,3), M_4 = (1,3)

Aufgabe b) habe ich erledigt, es ist ein Parallelogramm, da sowohl Vektor M_4 bis M_3 als auch Vektor M_1 bis M_2 Parallel sind → beide betragen (4,0) bzw. Vektor M_1 bis M_4 und Vektor M_2 bis M_3 betragen beide (1,3)

Wie sieht es aber mit der Aufgabe a) aus? Ich komme da nicht weiter...

Comments

Waren die 4 Eckpunkte so vorgegegeben oder hast du die selbst ausgesucht?

---

Diese Punkte waren vorgegeben. Habe nur die berechnete Version angegeben gehabt, habe die Punkte jetzt noch hinzugefügt, hatte ich vergessen zu machen.

Answer 1

Hallo,

berechne \(M_1+0,5\cdot\overrightarrow{M_1M_3}\)  und \(M_2+0,5\cdot\overrightarrow{M_2M_4}\)

Ergeben beide Rechnungen den gleichen Punkt, hast du die Halbierung gezeigt.

Gruß, Silvia

Comments

Die beiden Vektoren haben ja nicht dieselbe Länge, deshalb geht das nicht mal 0,5, oder?

Wenn ich das so wie du vorgegeben hast berechne kommt einmal (2,5, 0,5) und (1,5, 0,5) raus - also sie ergeben nicht denselben Punkt

DIe Angabe impliziert aber, dass hier eine Halbierung da sein muss

---

Die unterschiedlichen Längen spielen keine Rolle.

\(M_1+0,5\cdot\overrightarrow{M_1M_3}=\begin{pmatrix} 0\\0\end{pmatrix}+0,5\cdot\begin{pmatrix} 5\\3 \end{pmatrix}=\begin{pmatrix} 2,5\\1,5 \end{pmatrix}\\ M2+0,5\cdot\overrightarrow{M_2M_4}=\begin{pmatrix} 4\\0\end{pmatrix}+0,5\cdot\begin{pmatrix} -3\\3 \end{pmatrix}=\begin{pmatrix} 2,5\\1,5 \end{pmatrix}\\\)

---

Oh, dann habe ich mich verrechnet..

vielen vielen Dank!!