1. Aufgabe:
Mit reellen Parametern a, b und c ist die folgende Funktion gegeben:
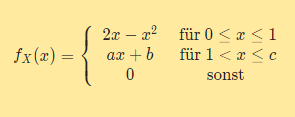
Text erkannt:
\( f_{X}(x)=\left\{\begin{array}{cc}2 x-x^{2} & \text { für } 0 \leq x \leq 1 \\ a x+b & \text { für } 1<x \leq c \\ 0 & \text { sonst }\end{array}\right. \)
Bestimmen Sie die Parameterwerte so, dass fX stetige Dichtefunktion einer Verteilungsfunktion FX ist; fX muss also stetig sein, und es muss gelten:
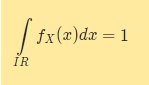
Text erkannt:
\( \int \limits_{I R} f_{X}(x) d x=1 \)
Problem/Ansatz:
Ich habe leider bei der Aufgabe keinen hinreichenden Ansatz, da diese sich komplett von den bisherigen Übungsaufgaben unterscheidet. Ich wäre sehr erfreut, wenn mir jemand den Lösungsweg aufzeigen könnte, damit ich das nachvollziehen kann.