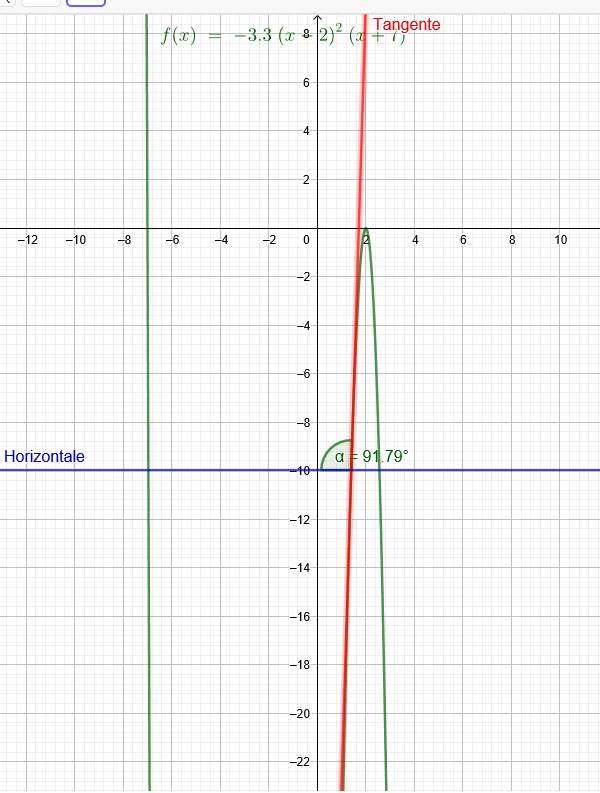
f(x) = a*[(x-2)2 *(x+7)]
Berechnen sie den Parameter a der Funktion so, dass die Tangente an f(x) bei x zur Horizontalen einschließt.
x₁= 1,4
Alpha= 88,2 Grad
tan(88,2°)≈31,8
f´(x) = a*[2*(x-2)*(x+7)+(x-2)2]
f´(1,4) = a*[2*(1,4-2)*(1,4+7)+(1,4-2)2]=-a*9,72
-9,72a=31,8
a=-\( \frac{31,8}{9,72} \)≈-3,3
f(x) = -3,3*[(x-2)2 *(x+7)]