Frage:
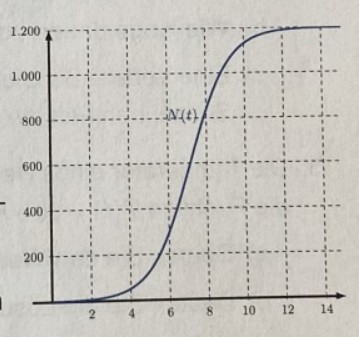
3. Eine Fast-Food-Kette eröffnet eine neue Filiale auf einem Universitätscampus. Unter den Studierenden kursiert das Gerücht, dass bei der Eröffnung ein berühmter Star ein Konzert geben wird. Die Funktion \( N(t) \) modelliert, wie viele Studierende das Gerücht \( t \) Tage nachdem es aufgekommen ist bereits kennen.
\( N(t)=\frac{1200}{1+1199 \cdot e^{-0,99 \cdot t}} \)
a) Lesen Sie ab wie viele Studierende es gibt.
b) Wie viele Studierende kennen das Gerücht nach 8 Tagen noch nicht?
c) Nach wie vielen Tagen kennen \( \frac{3}{4} \) aller Studierender das Gerücht?
d) Begründen Sie anhand der Grafik, an welchem Tag sich das Gerücht am schnellsten verbreitet.
Problem/Ansatz:
Das ganze Bespiel ist Hausaufgabe & da ich letzte Woche nicht anwesend sein konnte, weiß ich nicht wie es mit der Formel funktioniert… Kennt sich jemand aus?
Danke im Voraus!!!