Hallo Heinz,
hier nur eine 'schnelle' Antwort. Es lässt sich zeichnen ...
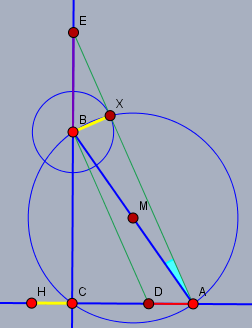
... also lässt es sich auch rechnen ;-) die gelbe Strecke soll \(h\) sein. Den Punkt \(X\) findet man als Schnittpunkt zweier Kreise und der Rest ist Vektorgeometrie oder geht auch mit linearen Funktionen.
Alternativ würde ich Dir aber einen anderen Lösungsweg vorschlagen.
Berechne zunächst den Winkel \(\angle XAB\) (hellblau) und schlage in zum Winkel \(\alpha = \angle BAC\) hinzu.$$c = \sqrt{a^2+b^2}\\\varphi =\angle XAB+\alpha = \arcsin\left(\frac hc\right) + \arctan\left(\frac ab\right)$$Der Winkel \(\varphi\) ist der Winkel der grünen Geraden \(e\) und \(f\) gegenüber der Horizontalen \(CA\). Und der Rest ist jetzt simple Trigonometrie$$|CE| = b \cdot \tan(\varphi) \implies a_1 =b \cdot \tan(\varphi)- a \\ |CD| = \frac{a}{\tan(\varphi)} \implies b_2 = b - \frac{a}{\tan(\varphi)}$$Das war's schon. Ich habe Dir das ganze mal in Desmos gegossen.
Du kannst die drei Werte für \(a\), \(b\) und \(h\) durch Verschieben der Punkte \(B\), \(A\) und \(H\) einstellen (\(h=|HC|\)). Die Ergebnisse für \(a_1\) und \(b_2\) werden jeweils angezeigt. Wenn Du auf das Desmos-Symbol drückst, so öffnet sich die App und Du kannst die Werte auch direkt oben links eintragen. Mit dem Mausrad kannst Du den Bildausschnitt anpassen.
Falls Du Fragen hast, so melde Dich bitte.
Gruß Werner