Signifikanztest gewürfelter Tetraeder

Question

Bei einem idealen Tetraeder tritt die 4 mit einer Wahrscheinlichkeit von \( p_0 = 0.25 \) auf. Wie muss bei einem zweiseitigen Test bei 200 Würfen und einem Signifikanzniveau von 5 % die Entscheidungsregel lauten? Testen Sie dazu die Nullhypothese \( H_0: p_0 = 0.25 \).

Ich bräuchte eine Lösung mit Erklärungen.

Answer 1

Die Anzahl der geworfenenen Vieren ist binomialverteilt mit den Parametern n=200 und p=0,25.

Damit kannst du für jede beliebige Trefferzahl von 0 bis 200 deren Wahrscheinlichkeit berechnen.

Wähle die Grenzen des Ablehnungsbereichs so, dass die Summe der Wahrscheinlichkeiten für 0, 1, 2, 3, usw Treffer kleiner als 0,025 bleibt.

Auch an der oberen Seite muss die Summe der Wahrscheinlichkeiten für 200, 199, 198, 197 usw. Treffer unter 0,025 bleiben.

Steht dir ein Rechenhilfsmittel mit Summenfunktion zur Verfügung oder musst du auf eine Annäherung mit Normalverteilung ausweichen?

Kleiner Tipp: der linke Ablehnungsbereich darf NICHT bis 38 gehen, denn dafür ist die Summe der Wahrscheinlichkeiten für 0 bis 38 Treffer geringfügig zu hoch.

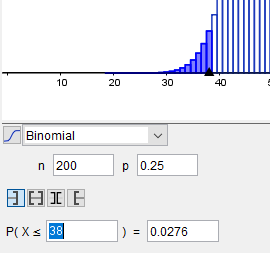
Rechne nach, dass stattdessen 0 bis 37 erlaubt ist!
Für den rechten Ablehnungsbereich suche die Grenze so im Bereich 60 ... 65.