Aufgabe:
Das anabole Steroid Testosteron steigert die Sauerstofftransportkapazität des Blutes und führt zu deutlichen
Leistungssteigerungen. Bei Dopingkontrollen wird die Testosteronkonzentration mit dem Normalwert
(NO = 679) verglichen. Der Quotient aus gemessenem Testosteronwert und Normalwert darf den Wert 4
nicht überschreiten, ansonsten gilt der Körper als gedopt. Da jeder menschliche Körper das zusätzliche
Testosteron mit der Zeit exponentiell mit unterschiedlichen Zerfallsfaktoren abbaut, sollten die
Dopingproben nicht zu lange nach der Einnahme des Mittels erfolgen. Es werden immer zwei Proben
entnommen, die A-Probe und die B-Probe.
Sehr häufig werden Anabolika unmittelbar vor einem Wettkampf eingenommen und die A-Probe
unmittelbar nach dem Wettkampfende entnommen. Die B-Probe wird einige Zeit später entnommen.
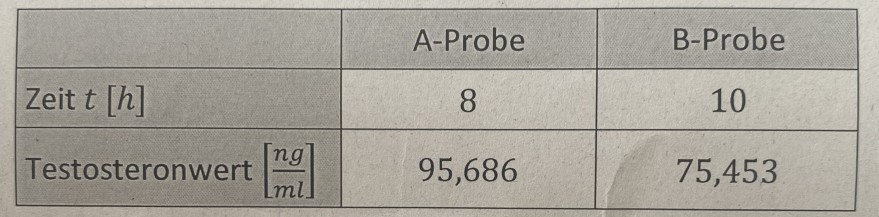
Bei einem Triathleten werden folgende Werte ermittelt:
1.
(8 Punkte) Bestimme die Funktionsgleichung ((t) = No + A • e'* der Testosteronkonzentration im
Blut in Abhängigkeit der Zeit nach der Einnahme des Steroids.
2. (4 Punkte) Ermittle die Halbwertzeit des Testosteronabbaus für den getesteten Triathleten.
3. (6 Punkte) Um die Einnahme des Dopingmittels zu verschleiern, kann die Einnahme auch einige Zeit
vor Wettkampfbeginn geschehen. Die Wirkung ist dann zwar nicht mehr so groß, dafür sind die
Ergebnisse der Proben negativ und der Sportler wird nicht bestraft. Berechne den Zeitpunkt vor
Wettkampfbeginn, an dem das Dopingmittel verabreicht werden muss, um der Bestrafung zu
entgehen.
4. (2 Punkte) Ein Testosteronwert von 240 n9 gilt als gesundheitsschädlich. Überprüfe, ob dieser Wert
durch die Einnahme des Dopingmittels überschritten wird.
Problem/Ansatz:
Kann mir eventuell jemand helfen bzw einen Ansatz finden? Komme schon bei Aufgabe 1 nicht weiter.