Grenzwerte und Herleitung

Question

Aufgabe:

Geben Sie eine nachvollziehbare Herleitung der Grenzwerte der folgenden Funktionen an.

f(x) = (2+x)^2⋅x−(5−x)^2
f(x) = 22x^2+1−5x^3 / (x−1)⋅(2x+5)⋅x
f(x) = ln( 1/e^-x )⋅√1+x^2

Problem/Ansatz:

Comments

Welcher Grenzwert? X gegen?

Außerdem solltest Du bei b durch Klammern deutlich machen, was zum Zähler bzw. Nenner des Bruchs gehört.

---

x=> +- unendlich

zur b) f(x)= (22x^2+1-5x^3) durch

                (x-1)•(2x+5)•x

Answer 1

f(x) = (2+x)^2⋅x−(5−x)^2 =( 4x + 4x^2 + x^3 - (25 - 10x + x^2 ) =x^3 +3x^2 + 14x -25

also für x gegen +∞ ist der GW +∞

also für x gegen -∞ ist der GW -∞.

Answer 2

f(x) = ln( \( \frac{1}{e^{-x}} \) )*\( \sqrt{1+x^{2}} \)

f(x) = ln( \( e^{x} \))*\( \sqrt{1+x^{2}} \)         ln( \( e^{x} \))=x

f(x) =x*\( \sqrt{1+x^{2}} \) 

\( \lim\limits_{x\to\infty} \)x*\( \sqrt{1+x^{2}} \)→∞

\( \lim\limits_{x\to-\infty} \)x*\( \sqrt{1+x^{2}} \)→-∞

Text erkannt:

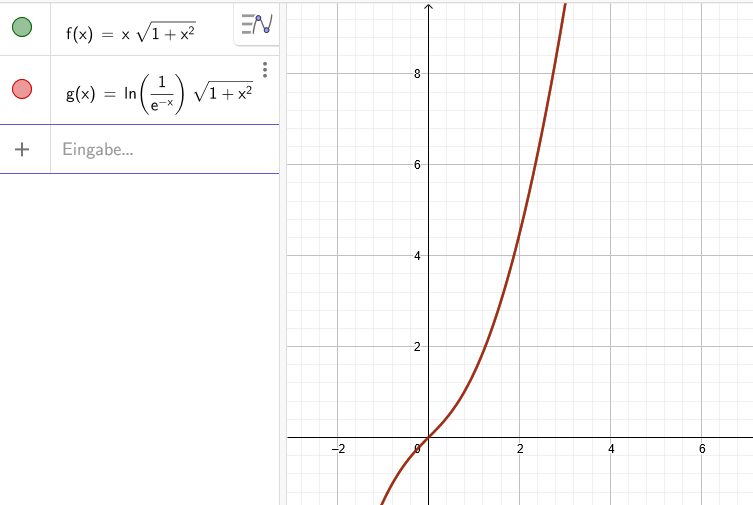
\( f(x)=x \sqrt{1+x^{2}} \quad \) ב̊ \( g(x)=\ln \left(\frac{1}{e^{-x}}\right) \sqrt{1+x^{2}} \)
\( +\quad \) Eingabe...

Comments

Grenzwert mit l´Hospital:

f(x)=\( \frac{22x^2+1-5x^3}{(x−1)⋅(2x+5)⋅x} \)

f(x)=\( \frac{-5x^3+22x^2+1}{2x^3+3x^2-5x} \)

\( \lim\limits_{x\to\infty} \)\( \frac{-5x^3+22x^2+1}{2x^3+3x^2-5x} \)=\( \lim\limits_{x\to\infty} \)\( \frac{-15x^2+44x}{6x^2+6x-5} \)=\( \lim\limits_{x\to\infty} \)\( \frac{-30x+44}{12x+6} \)=- \( \frac{5}{2} \)