Aufgabe:
ich habe Schwierigkeiten mit der unten dargestellten Aufgabe. Bei Teilaufgabe b) verstehe ich die 2 und die 3 nicht. Trotz Lösungen, die auch unten auf der letzten Seite dargestellt sind, kann ich den Rechenweg nicht nachvollziehen. Ich verstehe nicht wie man auf die Zahlen kommt (Es steht erst, dass 99 Plätze im Bus bebucht sind und eine Person ausfällt bzw. die Reise nicht antritt. Dann müssen es doch 98 Personen sein aber in der Tabelle bei b) in Teil 2) steht, dass es dann 97 sind. Das macht für mich keinen Sinn.).
Ich bitte um eine Erklärung. Vielen Dank im Voraus.
Liebe Grüße und schöne Ostertage

Text erkannt:
Abiturprüfung \( \mathbf{2 0 2 0} \)
Mathematik, Grundkurs
Prüfungsteil B: Aufgaben mit Hilfsmitteln
Aufgabenstellung:
Reisen mit dem Fernbus werden immer beliebter. Reiseanbieter werben mit günstigen Preisen und besonderem Komfort.
a) Für eine Städtereise stellt ein Busunternehmen einen Fernbus mit 59 Plätzen bereit, die vor Reiseantritt gebucht und bezahlt werden. Im Mittel werden \( 95 \% \) der Buchungen angetreten.
(1) Erläutern Sie, unter welcher Voraussetzung die Anzahl der angetretenen Buchungen bei einer Reise als binomialverteilt mit \( p=0,95 \) angenommen werden kann.
(2) Die Anzahl der angetretenen Buchungen wird als binomialverteilt mit \( p=0,95 \) vorausgesetzt. Für einen bestimmten Reisetermin sind genau 59 Buchungen vorgenommen worden.
Bestimmen Sie jeweils die Wahrscheinlichkeit für folgende Ereignisse:
\( E_{1} \) : Genau 59 Buchungen werden angetreten.
\( E_{2} \) : Mindestens 55 Buchungen werden angetreten.
\( E_{3}: \) Mehr als 6 Buchungen werden nicht angetreten.

Text erkannt:
(3) Obwohl Buchungen insgesamt mit einer Wahrscheinlichkeit von \( 5 \% \) nicht angetreten werden, treten Reisende unter 50 Jahren eine Buchung deutlich häufiger nicht an als Reisende über 50 Jahren. [Reisende, die genau 50 Jahre alt sind, werden zur Gruppe der Reisenden über 50 Jahren gezählt.]
Die Wahrscheinlichkeit, dass eine Buchung nicht angetreten wird, betrage bei Reisenden unter 50 Jahren \( 6 \% \), bei Reisenden über 50 Jahren nur \( 2 \% \).
(i) Geben Sie auf den waagerechten Strichen die fehlenden Wahrscheinlichkeiten im folgenden Baumdiagramm an.
U50: Reisende unter 50 Jahren \( \quad A \) : Antreten der Buchung
Ü50: Reisende über 50 Jahren \( \quad \bar{A}: \) Nichtantreten der Buchung
(ii) Ein Reisender wird zufällig ausgewählt.
Ermitteln Sie die Wahrscheinlichkeit \( x \), dass es sich um einen Reisenden unter 50 Jahren handelt.
[Kontrolllösung: \( x=0,75 \) ]
(iii) Ermitteln Sie die Wahrscheinlichkeit, dass es sich bei der Buchung eines Reisenden, der die Buchung nicht antritt, um einen Reisenden unter 50 Jahren handelt.
(3+9+8 Punkte)

Text erkannt:
b) Da erfahrungsgemäß nicht alle Buchungen angetreten werden, verkauft das Busunternehmen mehr Plätze als vorhanden sind. Für eine Städtereise mit 96 Plätzen werden 99 Buchungen vorgenommen (Überbuchung). Vereinfachend wird wieder angenommen, dass die Anzahl der angetretenen Buchungen binomialverteilt mit \( p=0,95 \) ist.
(1) Ermitteln Sie die Wahrscheinlichkeit, dass mindestens eine Person ihre Reise wegen Überbuchung nicht antreten kann.
Kann eine Person die Reise wegen Überbuchung nicht antreten, wird vom Busunternehmen der komplette Reisepreis von 20 Euro zurückerstattet. Als Entschädigung wird zusätzlich ein Betrag von 300 Euro ausgezahlt.
(2) Das Busunternehmen erfasst Werte zur Überbuchung in der folgenden Tabelle.
Ermitteln Sie die in der Tabelle fehlenden Werte.
\begin{tabular}{|c|c|c|c|}
\hline Anzahl der Personen, die wegen Überbuchung nicht antreten können & 1 & 2 & 3 \\
\hline Anzahl \( k \) der angetretenen Buchungen & 97 & 98 & 99 \\
\hline\( P_{99 ; 0,95}(X=k) \) & & & \\
\hline Kosten für Erstattung und Entschädigung in \( € \) & 320 & & \\
\hline
\end{tabular}
(3) Beurteilen Sie, ob sich aus finanzieller Sicht die Praxis, 99 Buchungen für eine Reise mit 96 Plätzen zu bestätigen, für das Busunternehmen im Mittel lohnt.
\( (3+5+4 \text { Punkte) } \)
Text erkannt:
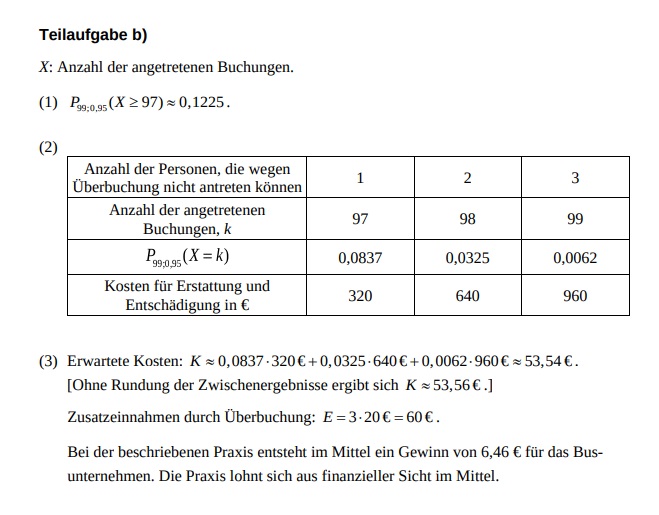
Teilaufgabe b)
\( X \) : Anzahl der angetretenen Buchungen.
(1) \( P_{99 ; 0,95}(X \geq 97) \approx 0,1225 \).
(2)
\begin{tabular}{|c|c|c|c|}
\hline Anzahl der Personen, die wegen Überbuchung nicht antreten können & 1 & 2 & 3 \\
\hline Anzahl der angetretenen Buchungen, \( k \) & 97 & 98 & 99 \\
\hline\( P_{99 ; 0,95}(X=k) \) & 0,0837 & 0,0325 & 0,0062 \\
\hline Kosten für Erstattung und Entschädigung in \( € \) & 320 & 640 & 960 \\
\hline
\end{tabular}
(3) Erwartete Kosten: \( K \approx 0,0837 \cdot 320 €+0,0325 \cdot 640 €+0,0062 \cdot 960 € \approx 53,54 € \).
[Ohne Rundung der Zwischenergebnisse ergibt sich \( K \approx 53,56 € \).]
Zusatzeinnahmen durch Überbuchung: \( E=3 \cdot 20 €=60 € \).
Bei der beschriebenen Praxis entsteht im Mittel ein Gewinn von 6,46 \( € \) für das Busunternehmen. Die Praxis lohnt sich aus finanzieller Sicht im Mittel.
Problem/Ansatz:
Ich habe einen Ansatz aber verstehe die Lösung nicht.