Fläche, die von den Graphen der Funktionen eingeschlossen wird

Question

Aufgabe:

Berechne den Inhalt der vom Graphen der Funktion f und der Geraden G begrenzten Fläche !

f(x)=4-x^2

g:y=-2

Answer 1

Beide Funktionen um 2 Einheiten nach oben verschieben:

\(f(x)=6-x^2\)      und \( g(x)=0\)

Nullstellen:  \(x₁=\sqrt{6} \)     \(x₂=-\sqrt{6} \)

Da die Parabel symmetrisch zur y-Achse ist:

\(A=2*\int\limits_{0}^{\sqrt{6}}(6-x^2)*dx=\int\limits_{0}^{\sqrt{6}}(12-2*x^2)*dx\)

\(A=12*x- \frac{2}{3}*x^3=x*(12-\frac{2}{3}*x^2)=\sqrt{6}*(12-4)\)

\(A=8*\sqrt{6}\)

Comments

Hast du 4-x^2 + 2 gemacht ?

---

So ist es! Auch die Gerade ist 2 Einheiten nach oben verschoben worden.

---

Wieso hast du bei der Fläche mal 2 gemacht ?

---

Wieso hast du bei der Fläche mal 2 gemacht ?

Das stand hier:

Da die Parabel symmetrisch zur y-Achse ist

hat er erst einmal nur die Hälfte der Fläche berechnet. Das Einsetzen der Integrationsgrenze 0 ist rechnerisch wesentlich einfacher als das Einsetzen von\( -\sqrt{6} \).

Answer 2

Schnittpunkte von f und g bestimmen (bei x = \( \pm \sqrt{6} \))

Integrieren von g(x) - f(x) von x = \(-\sqrt{6}\) bis x = \(\sqrt{6}\) (ich komme auf \( 8\sqrt{6} \))

Fertig.

Answer 3

Hallo,

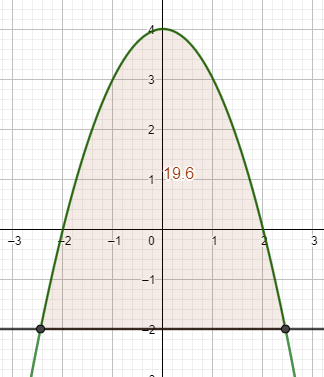
\( \begin{aligned} f(x) &=4-x^{2} \\ g(x) &=-2 \\[10pt] \text{Differenzfunktion bilden:}\\h(x) &=f(x)-g(x) \\ &=4-x^{2}-(-2) \\ &=4-x^{2}+2 \\ &=6-x^{2} \\[10pt] \text{Integrationsgrenzen bestimmen:}\\6-x^{2} &=0 \\-x^{2} &=-6 \\ x^{2} &=6 \\ x &=\pm \sqrt{6} \end{aligned} \)

Stammfunktion aufstellen:

\( \begin{aligned} H(x)=6 x-\frac{1}{3} x^{3} \\ H(+\sqrt{6}) &=6 \cdot \sqrt{6}-\frac{1}{3} \cdot \sqrt{6}^{3} \\ &=6 \sqrt{6}-\frac{1}{3} \cdot 6 \cdot \sqrt{6} \\ &=6 \sqrt{6}-2 \sqrt{6} \\ &=4 \sqrt{6} \end{aligned} \)

\( \begin{aligned} H(-\sqrt{6}) &=6 \cdot(-\sqrt{6}) \cdot \frac{1}{3} \cdot(-\sqrt{6})^{3} \\ &=-6 \sqrt{6}-\frac{1}{3} \cdot 6 \cdot(-\sqrt{6}) \\ &=-6 \sqrt{6}+2 \sqrt{6} \\ &=-4 \sqrt{6} \end{aligned} \)

\( \begin{aligned} A=H(\sqrt{6})-H(-\sqrt{6}) &=4 \sqrt{6}-(-4 \sqrt{6}) \\ &=8 \sqrt{6} \end{aligned} \)

Gruß, Silvia