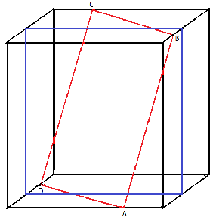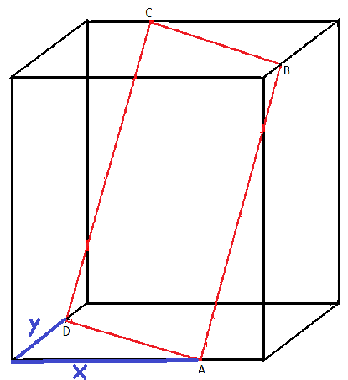
Wir können nicht unbedingt davon ausgehen, dass alle 4 Punkte ihre Würfelkante im selben Verhältnis teilen, da AD und BC auf der Oberfläche liegen, während AB und CD quer durch den Würfel gehen. Ich setze die Länge der Würfelkante mit 1 und die Längen der eingezeichneten Teilstrecken mit x bzw. y.
Diese beiden Längen in der Grundfläche unten links vorn nehme ich auch (nicht eingezeichnet) in der Deckfläche (oben recht hinten) an.
Dann gilt AD =\( \sqrt{x^2+y^2} \) und BC = \( \sqrt{(1-x)^2+1^2+(1-y)^2} \).
Das kann gleichgesetzt werden, es ergibt sich
0=3-2x-2y bzw. x=1,5-y.
Die Länge von AD lässt sich damit nur mit y als \( \sqrt{2,25-3y+y^2+y^2} =\sqrt{2,25-3y+2y^2} \) schreiben
Ich teste, ob sich damit immer ein rechter Winkel zwischen AD und AB ergibt. Der Abstand DB ist
\( \sqrt{(y-(1-y))^2+1^2+1^2} =\sqrt{(2y-1))^2+2} =\sqrt{4y^2-4y+3} \).
Im Falle eines Quadrates muss BD das \( \sqrt{2} \)-fache von AB bzw. (BD)² das Doppelte von (AB)² sein.
Ich setze deshalb
\(4y^2-4y+3 = 2 (2,25-3y+2y^2)\) an und erhalte nach Subtraktion von 4y²
3-4y=4,5-6y und damit y=3/4. Wegen x=1,5-y ist auch x=3/4 (und somit entgegen meiner anfänglichen Vermutung doch gleich y).
Das ist überhaupt die EINZIGE Möglichkeit, mit den Punkten A,B,C,D auf ihren in der Zeichnung vorgegebenen Kanten ein Quadrat zu erzeugen. Damit gibt es keine Möglichkeit, y jetzt noch zum Zwecke einer Flächenmaximierung zu variieren.
Die Würfelkante wird jeweils im Verhältnis 3:1 geteilt.
Es sind nur kleinere Quadratflächen möglich, wenn die Schnittebene parallel zu einer der Würfelflächen verläuft: