Aufgabe:
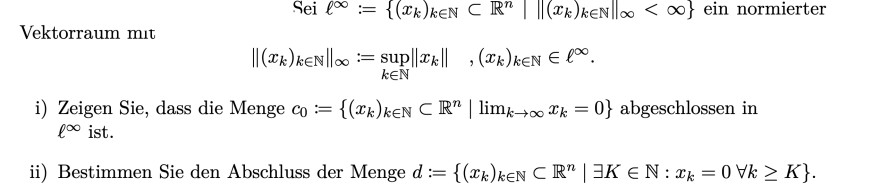
Text erkannt:
Vektorraum mit
\( \left\|\left(x_{k}\right)_{k \in \mathbb{N}}\right\|_{\infty}:=\sup _{k \in \mathbb{N}}\left\|x_{k}\right\| \quad,\left(x_{k}\right)_{k \in \mathbb{N}} \in \ell^{\infty} . \)
i) Zeigen Sie, dass die Menge \( c_{0}:=\left\{\left(x_{k}\right)_{k \in \mathbb{N}} \subset \mathbb{R}^{n} \mid \lim \limits_{k \rightarrow \infty} x_{k}=0\right\} \) abgeschlossen in \( \ell^{\infty} \) ist.
ii) Bestimmen Sie den Abschluss der Menge \( d:=\left\{\left(x_{k}\right)_{k \in \mathbb{N}} \subset \mathbb{R}^{n} \mid \exists K \in \mathbb{N}: x_{k}=0 \forall k \geq K\right\} \).
Problem/Ansatz:
zu i): Wie würde man hier am besten die Abgeschlossenheit zeigen? Über das Komplement?
zu ii): Wäre der Abschluss nicht alles echt kleiner 0? Wie würde man das aber zeigen?