Quadrat zeichnen und Eckpunktkoordinaten ablesen

Question

Aufgabe:

Von einem Quadrat mit den Eckpunkten \( A, B, C \) und \( D \) sind der Eckpunkt \( C=(5 \mid-3) \) und der Schnittpunkt der Diagonalen \( M=(3 \mid 1) \) gegeben. Die Eckpunkte \( A, B, C \) und \( D \) des Quadrats sind dabei gegen den Uhrzeigersinn angeordnet.

Aufgabenstellung: Ermitteln Sie die Koordinaten der Eckpunkte \( A \) und \( B \).

\( A= \)
\( B= \)

Problem/Ansatz:

Wie komm ich hier auf den Punkt B? Den Punkt A hab ich schon

Comments

Den Punkt A hab ich schon

Nämlich mit welchen Koordinaten?

Answer 1

Zeichne die beiden Punkte mal in ein Koordinatensystem ein und lade das hier hoch. Dann siehst Du die Lösung viel klarer.

Comments

Der Punkt B soll (1,1) sein. Das schaut komisch aus

---

Der Punkt B soll (1,1) sein. Das schaut komisch aus

Ich meine die Punkte C und M.

In ein Koordinatensystem eintragen und hier hochladen...

---

~draw~ punkt(5|-3 "C")%1.5%;punkt(3|1 "M")%1.5%;punkt(1|5 "A")%1.5%;punkt(7|3 "D")%1.5%;punkt(-1|-1 "B")%1.5%;polygon(1|5 -1|-1 5|-3 7|3)#;linienzug(1|5 5|-3);polygon(-1|-1 7|3);;polygon(x|y x|y …);polygon(x|y x|y …);polygon(x|y x|y …);polygon(x|y x|y …);polygon(x|y x|y …);zoom(10) ~draw~

Answer 2

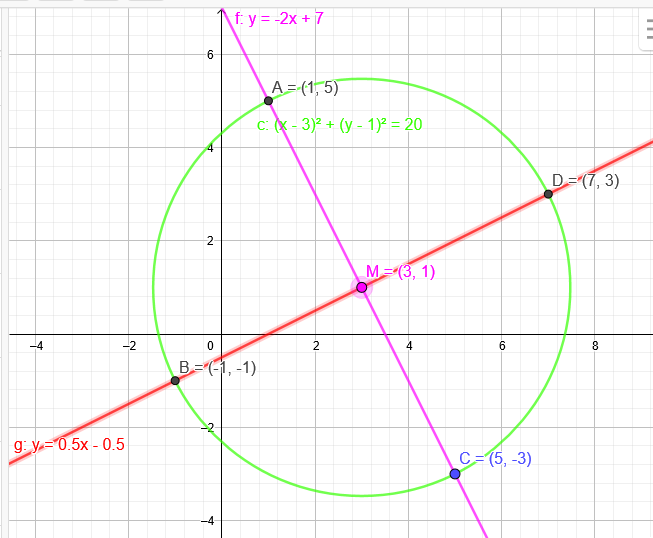
1.) Gerade durch \( M=(3 \mid 1) \) und \( C=(5 \mid-3) \)   

\(y=-2x+7 \)

2.) Kreis um \( M=(3 \mid 1) \) mit \( C=(5 \mid-3) \) ∈ Kreis

\( (x-3)^2+(y-1)^2=20\)

3.) \( (x-3)^2+(y-1)^2=20\) schneidet \(y=-2x+7 \) in \( A=(1 \mid 5) \)

4.)Normale zu \(y=-2x+7 \) durch \( M=(3 \mid 1) \)

\(y=0,5x-0,5\) schneidet den Kreis \( (x-3)^2+(y-1)^2=20\)   in \( B=(-1 \mid -1) \)  und  \( D=(7 \mid 3) \)