Steckbriefaufgabe kubische Funktion

Question

Aufgabe:

Gleichung bestimmen

Gleichung dritten Grades mit folgenden Punkten

g(-2)  = 0

g ' (-2) = - 5

g ' (2) = -9

g(0) = 0

Problem/Ansatz:

Ich komme nicht voran..

Danke!!

Comments

4 Unbekannte und nur 3 Bedingungen... Fehlt da vielleicht noch eine Bedingung?

---

Wie war denn der originale Aufgabentext ?

Vielleicht kann man da noch eine Bedingung rauskitzeln.

---

Gleichung geht durch den Ursprung.

g(0)=0

Answer 1

Aloha :)

Da zwei Nullstellen \((0|0)\) und \((-2|0)\) bekannt sind, kannst du den verkürzten Ansatz wählen:$$g(x)=(x-0)\cdot(x+2)\cdot(ax+b)$$Zum einfachen Ableiten rechnen wir dies aus:$$g(x)=x\cdot(ax^2+2ax+bx+2b)=ax^3+2ax^2+bx^2+2bx$$$$\phantom{g(x)}=ax^3+(2a+b)x^2+2bx$$

Die Ableitung lautet:$$g'(x)=3ax^2+2(2a+b)x+2b$$Wir setzen die beiden Forderungen ein:$$-5\stackrel!=g'(-2)=4a-2b$$$$-9\stackrel!=g'(\phantom-2)=20a+6b$$Dieses kleine Gleichungssystem hat die Lösung:\(\quad a=-\frac34\quad;\quad b=1\)

Daher lautet die gesuchte Funktion:$$g(x)=-\frac34x^3-\frac12x^2+2x$$

~plot~ -3/4*x^3-x^2/2+2x ; {0|0} ; {-2|0} ;  ~plot~

Answer 2

Benutze http://www.arndt-bruenner.de/mathe/scripts/steckbrief.htm zur Hilfe und Selbstkontrolle

Eigenschaften

f(0) = 0
f(-2) = 0
f'(-2) = -5
f'(2) = -9

Gleichungssystem

d = 0
-8a + 4b - 2c + d = 0
12a - 4b + c = -5
12a + 4b + c = -9

Errechnete Funktion

f(x) = -0,75·x^3 - 0,5·x^2 + 2·x

Comments

Korrektur bei den eigenschaften

f ' (2) = - 5

Kannst du mir eventuell erklären wie man auf das gleichungssystem kommt? Also die 8, 4 etc. woher weiss man das?

Dankee

---

Der Ansatz ist

f(x) = a·x^3 + b·x^2 + c·x + d
f'(x) = 3·a·x^2 + 2·b·x + c

Daraus leitest du jetzt die Gleichungen her

f(-2) = 0
a·(-2)^3 + b·(-2)^2 + c·(-2) + d = 0
a·(-8) + b·(4) + c·(-2) + d = 0
-8a + 4b - 2c + d = 0

Ist das soweit klar?

---

Super, dankee

Answer 3

Gleichung dritten Grades

\(g(x) = ax^3 + bx^2 + cx + d\)

Übrigens: Funktionsgleichung.

g(-2)  = 0

(1)        \(a\cdot (-2)^3 + b\cdot (-2)^2 + c\cdot (-2) + d = 0\)

g ' (-2) = - 5

\(g'(x) = 3ax^2 + 2bx + c\)

(2)        \(3a\cdot (-2)^2 + 2b\cdot (-2) + c = -5\)

g ' (2) = -9

(3)        \(3a\cdot 2^2 + 2b\cdot 2 + c = -9\)

g(0) = 0

(4)        \(a\cdot 0^3 + b\cdot 0^2 + c\cdot 0 + d = 0\)

Answer 4

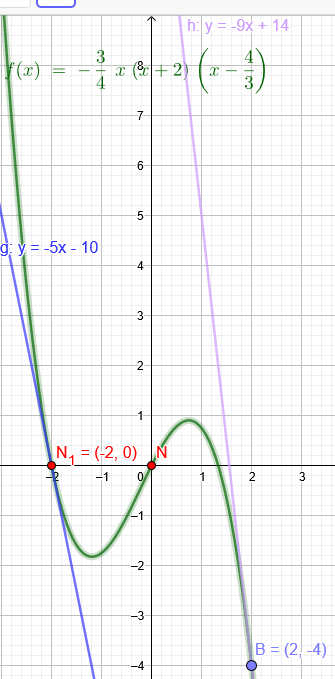
Gleichung dritten Grades mit folgenden Punkten \(g(-2)  = 0\)    \(g ' (-2) = - 5\)
\(g ' (2) = -9\)     \(g(0) = 0\)

\(g(x)=a*[x*(x+2)*(x-N)]\)

\(g´(x)=a*[(x+2)*(x-N)+x*(x-N)+x*(x+2)]\)

\(g´(-2)=a*[4+2N]\)

\(a*[4+2N]=-5→a=-\frac{5}{4+2N}\)

\(g´(2)=-\frac{5}{4+2N}*[(2+2)*(2-N)+2*(2-N)+2*(2+2)\)]

\(\frac{5}{4+2N}*(20-6N)=9\)

\(N=\frac{4}{3}\)

\(a=-\frac{5}{4+2*\frac{4}{3}}=-\frac{3}{4}\)

\(g(x)=-\frac{3}{4}*x*(x+2)*(x-\frac{4}{3})\)