Ich habe in der Schule eine Aufgabe gekriegt welche folgender Maßen lautete:
A)
Fünf Karten sind auf der Oberseite schwarz, auf der Unterseite weiß. Man legt sie vor sich, die Seite bei allen nach oben. Nun nimmt man zwei Karten auf und dreht sie um so dass die weiße Seite oben liegt. Nun dreht man wieder zwei Karten um. Jetzt können wieder drei Schwarze und drei weiße Seiten oben liegen. Man wiederholt diesen Vorgang solange wie man will. Kann man auf diese Weise erreichen, dass schließlich alle weißen Seiten oben liegen?
diese Teilaufgabe löste ich folgendermaßen:
Vorausetzung: (Gegeben)
- 5 karten (a, b, c, d, e), können entweder Wert "1" (weiß) oder Wert "0" (schwarz) haben.
- alle karten starten mit wert 0 (schwarz)
- pro zug ändern 2 ausgewählte Karten ihren Wert (1 wird zu 0, 0 wird zu 1)
Frage: (Gesucht, Behauptung)
Kann man auf diese Weise erreichen, das alle Karten gleichzeitig den Wert "0" haben?
Antwort: (Lösung, Lösungsweg)
Nein. Es geht nicht, weil:
Im 1. Zug hat man eine Möglichkeit etwas zu tun:
1. Es werden 2 von 5 Karten auf den Wert 1 gedreht.
In dieser Position 2 kann man 3 Dinge tun:
1. Man kann diese Position halten, indem man eine 0er und eine 1er Karte dreht.
2. Man kann wieder zur Anfangsposition (alles 0) gehen, indem man zwei 1er Karten umdreht.
3. Man kann zu der 3. Position gehen (4 Karten haben den Wert 1) indem man zwei Karten wendet, welche den Wert 0 haben
Da Möglichkeiten 1 und 2 zu sich selber führen hat man nur die logische Möglichkeit Möglichkeit 3 zu wählen.
In der Position 3 kann man 2 dinge tun:
1. Man kann die Position halten, indem man eine 1er Karte und die letzte verbleibende 0er Karte wendet
2. Man kann zu Position 2 Übergehen indem man zwei 1er Karten wendet.
Dies führt zu einem Loop. Es gibt keine Möglichkeit 5 Karten gleichzeitig auf Wert 1 zu haben.
Teilaufgabe B konnte ich auch ziemlich einfach lösen:
b)
Statt zwei dreht man stets drei Karten um. Lässt sich so erreichen, das schließlich alle weißen Seiten oben liegen?
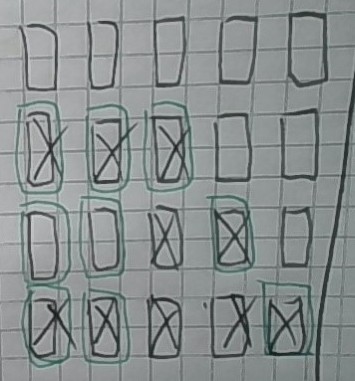
(Ich weiß nicht ob das als Handschriftliche Notiz gilt aber ich lads mal hoch)
Ja. Folgendermaßen:
Zuerst dreht man abc auf "1"
anschließend dreht man ab auf "0" und d auf "1"
danach dann ab und e auf "1" und alle karten sind weiß.
dann kam ein ganz fetter brocken.
c)
Nun hast du n Karten bei denen die Oberseite schwarz und die Unterseite weiß ist. Es dürfen immer k Karten umgedreht werden. Für welche Zahlenpaare (n;k) kann man schließlich erreichen, dass alle weißen Seiten oben liegen? Für welche ist dies nicht möglich? Beweise deine Antwort.
Ich habe erstmal ein bissel rumprobiert und bin zu dem Schluss gekommen, das man alle weiß erreichen kann wenn:
k ungerade aber n gerade
k gerade aber n ungerade
k ungerade und n ungerade
k gerade und n gerade
sind.
Es geht nicht wenn
k gerade aber n ungerade ist.
Ich habe aber keinen Schimmer wie ich das beweisen soll oder ob es überhaupt richtig ist.
Ich würde mich sehr über Hilfe bei Aufgabe c) freuen :D
Vielen Dank im Voraus
