Hallo,
in einem regelmäßigen Sechseck bildet der Mittelpunkt \(M\) mit einer der Seiten ein regelmäßigen Dreieck (z.B. \(\triangle ABM\)). Sei die Länge einer Seite \(a\), so ist auch die Strecke vom Mittelpunkt zu einer der Ecken \(=a\).
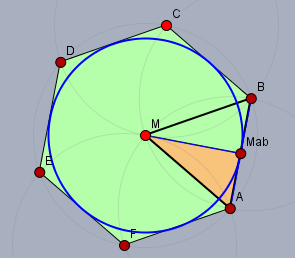
Mit \(r\) als Radius des Inkreis gilt Im braunen rechtwinkligen Dreieck \(\triangle AM_{ab}M\) der Pythagoras$$a^2 = r^2 + \left(\frac{a}{2}\right)^2 \implies a = \frac{2}{3}\sqrt{3}\,r = \frac{2}{\sqrt 3} r$$Die Fläche \(F\) des Sechsecks ist 6-mal die Fläche eines der gleichseitigen Dreiecke$$F = 6\cdot \frac 12 ra = 3 r \cdot \frac{2}{3}\sqrt{3}\,r = 2\sqrt{3}\,r^2$$
Bestimmen Sie die Ableitung des Flächeninhalts des regelmäßigen
Sechsecks nach dem Radius des Inkreises ohne Formeln zu verwenden.
Na ja, wenn $$F(r) = 2\sqrt{3}\,r^2$$dann ist$$F'(r) = 4\sqrt{3}\,r$$natürlich habe ich dabei die Regeln des Ableitens angewendet (gilt das als Formel?).
Ohne jede Formel lässt sich aber sofort sagen, dass $$F'(r) \propto r$$also die Ableitung der Fläche ist proportional zum Radius \(r\) bzw. genau der Umfang des Sechsecks. Also$$F'(r) = 6a = 6 \cdot \frac{2}{3}\sqrt{3}\,r = 4\sqrt{3} \,r$$Gruß Werner