Bestimmen Sie \lambda ∈ ℝ so, dass \vec{x}+\lambda \vec{y} senkrecht auf \vec{z} steht.

Question

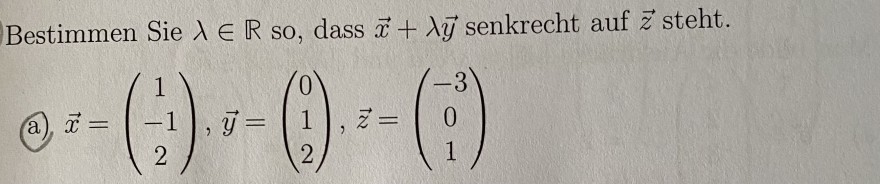
Text erkannt:

Bestimmen Sie \( \lambda \in \mathbb{R} \) so, dass \( \vec{x}+\lambda \vec{y} \) senkrecht auf \( \vec{z} \) steht.
a) \( \vec{x}=\left(\begin{array}{c}1 \\ -1 \\ 2\end{array}\right), \vec{y}=\left(\begin{array}{l}0 \\ 1 \\ 2\end{array}\right), \vec{z}=\left(\begin{array}{c}-3 \\ 0 \\ 1\end{array}\right) \)

Aufgabe:

Problem/Ansatz

Wie löst man diese Aufgabe?

Answer 1

Hallo

senkrecht heisst Skalarprodukt =0 also <x+λy,z>=0

lul

Answer 2

Rechne Skalarprodukt zwischen x+lambda*y , was (1/-1+k/2+k) ist, und z

(k steht für lambda) in Abhängigkeit von lambda , dann setze das Skalarprodukt gleich 0, indem du Skalarpdukt nach k umstellst.

Comments

Danke Aki57!