Intervallhalbierungsmethode mit e = 0,1 anwenden

Question

Guten Abend, leider kenne ich mich bei diesem Beispiel nicht aus. Mir wäre es aber wichtig zu wissen wie es funktioniert, daher hier ist mal das Beispiel.

Zeigen Sie, dass die durch

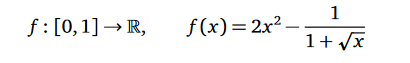
Text erkannt:

\( f:[0,1] \rightarrow \mathbb{R}, \quad f(x)=2 x^{2}-\frac{1}{1+\sqrt{x}} \)

definierte Funktion mindestens einen Fixpunkt besitzt. Bestimmen Sie den/einen Fixpunkt mit Hilfe der Intervallhalbierungsmethode bis auf einen Fehler von ε = 0,1.

Mir wäre wichtig zu verstehen, wie ich die Intervallhalbierungsmethode auf das obige Beispiel anwenden kann. Vielen Dank für eure Hilfe.

Answer 1

Leider falsch, Danke an Arsinoe, Berichtigung folgt.

f(0)=-1<0, f(1)=1,5>0

Intervall halbiert f(1/2)=-0,08<0   damit sind wir schon beim Fehler <0,1

aber als nächstes käme wieder das Intervall zwischen positivem und negativem Wert halbieren also f(0,75) >0

zwischen 0,5 und 0,75

das heisst du halbierst immer den Wert zischen dem positiven und negativen Wert.

Gruß lul

Comments

Es geht um Fixpunkte von ƒ, nicht um Nullstellen.

---

Hallo

Fixpunkte sind Nullstellen von f(x)-x=0

aber ich sehe, ich habe einen Fehler gemacht.

g(x)=f(x)-x=0 g(0)=-1<0 g(1)=0,5>0

Halbierung: g(0,5)=-0,58<0

Halbierung : g(0,75)=-0,16

Halbierung g(0,875)=0,14

Mitte g(0,8125)=....

Gruß lul

---

Also sind das die Fixpunkte nun?