Hallo,
Falls Du nicht weißt, wie man zum Schnittpunkt \(S=(5|\,-2)\) der Geraden \(g\) und \(h\) kommt, so melde Dich bitte noch einmal!
Für die Berechnung der Tangenten von \(S\) an den Kreis gibt mehrere unterschiedliche(!) Möglichkeiten diese Aufgabe zu lösen. Eine davon hat oswald bschrieben.
Eine zweite besteht darin, die Gerade \(t\) durch den Schnittpunkt \(S=(5|\,2)\) zu bestimmen. In der Punkt-Steigungsform ist:$$t:\quad y=m(x-5)-2$$mit der noch unbekannten Steigung \(m\). Diese wird in die Kreisgleichung eingesetzt:$$x^{2} + (m(x-5)-2-3)^{2} = 5$$und im weiteren nach \(x\) aufgelöst. Hier bekommt man im Allgemeinen zwei Lösungen, da eine Gerade einen Kreis zweimal schneiden kann:$$\begin{aligned} x^{2} + (m(x-5)-2-3)^{2} &= 5\\ x^2 + (mx-(5m+5))^2 &= 5 \\ x^2 + m^2x^2 -2mx(5m+5) + (5m+5)^2 &= 5\\ x^2(1 + m^2) -2mx(5m+5) + ((5m+5)^2 -5) &= 0\\ \end{aligned}\\x_{1,2} = \frac{2m(5m+5) \pm \sqrt{4m^2(5m+5)^2 - 4\cdot(1 + m^2)\cdot((5m+5)^2 -5) }}{2(1+m^2)} $$da wir nicht zwei Schnittpunkte "Gerade mit Kreis" sondern den Berührpunkt der Tangente mit dem Kreis suchen, interessiert hier nur der Fall, bei dem \(x\) nur genau eine Lösung hat. Und dies ist der Fall, wenn der Ausdruck unter der Wurzel =0 wird. Also:$$\begin{aligned}0&= 4m^2(5m+5)^2 - 4\cdot(1 + m^2)\cdot((5m+5)^2 -5)\\ 4m^2(5m+5)^2 &= 4\cdot(1 + m^2)\cdot((5m+5)^2 -5)\\ m^2(5m+5)^2 &= ((5m+5)^2 -5) + m^2(5m+5)^2 -5m^2\\ 0&= (5m+5)^2 -5 -5m^2\\ 0&= 5(m+1)^2 -1 -m^2\\ 0&= 5(m^2+2m+1) -1 -m^2\\ 0&= 5m^2+10m+5 -1 -m^2\\ 0&= 4m^2+10m+4 \\ 0&= m^2+\frac52 m+1 \\ m_{1,2} &= -\frac54 \pm \sqrt{\frac{25}{16} - 1} \\ &= -\frac54 \pm \frac 34 \\ m_1 &= -\frac12, \quad m_2 = -2 \end{aligned}$$Also sind die beiden Tangenten:$$t_1:\quad y=-\frac12(x-5)-2 = \frac12 x + \frac12\\t_2: \quad y= -2(x-5)-2 = -2x+8$$
Die dritte Methode und die zweite, die ich Dir hier vorstelle, ist von der Rechnung her viel einfacher als die ersten beiden. Es setzt aber voraus, dass Du weißt, was die Normalenform einer Gerade ist und sie verlangt ein wenig Trigonometrie samt rudimentere Vektorrechnung. Dazu folgende Skizze:
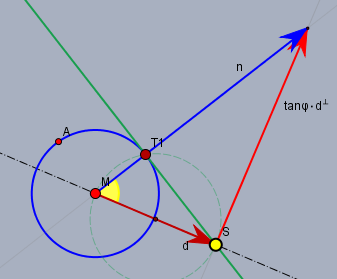
Dort siehst Du den Kreis (blau), den Punkt \(S\) (gelb) und eine der Tangenten (grün) durch \(S\) an den Kreis. Die Normalform einer Gerade durch \(S\) mit dem Normalenvektor \(\vec n\) lautet$$\vec n \vec x = \vec n S$$das ist genau wie bei der Geraden \(h\)$$x+y= 3 \quad \to \begin{pmatrix} 1\\1 \end{pmatrix} \vec x= 3 \quad \to \begin{pmatrix} 1\\1 \end{pmatrix} \vec x=\begin{pmatrix} 1\\1 \end{pmatrix}\begin{pmatrix} 0\\3 \end{pmatrix}$$Die \(3\) rechts ist auch nur das (Skalar)produkts mit \(\vec n=\begin{pmatrix} 1\\1 \end{pmatrix}\) und einem Punkt \(\begin{pmatrix} 0\\3 \end{pmatrix}\), durch den die Gerade verläuft.
Wir benötigen also "nur" den Vektor \(\vec n\) und das ist der blaue Vektor im Bild, der sich aus einer Vektorsumme zusammen setzt:$$\vec n = \vec d \pm \tan(\varphi) \cdot \vec d^{\perp}$$\(\vec d\) ist der Vektor von \(M\) nach \(S\) und \(\vec d^{\perp}\) ist ein Vektor gleicher Länge, der senkrecht auf \(\vec d\) steht. \(\varphi\) ist der gelbe Winkel bei \(M\). Das \(\pm\) kommt daher, da man die ganze Figur an der Geraden durch \(M\) und \(S\) spiegeln kann. Es ist$$\vec d = S - M = \begin{pmatrix} 5\\-2 \end{pmatrix} - \begin{pmatrix} 0\\3 \end{pmatrix} = \begin{pmatrix} 5\\-5 \end{pmatrix}\\ \vec d^{\perp} = \begin{pmatrix} -d_y\\d_x \end{pmatrix} = \begin{pmatrix} 5\\5 \end{pmatrix}$$und \(\tan(\varphi)\) folgt aus dem Dreieck \(\triangle MST_1\)$$\tan(\varphi) = \frac{|ST_1|}{r} = \frac 1r \sqrt{\vec d^2 - r^2} = \sqrt{\frac{\vec d^2}{r^2}-1}$$nach dem Vorgeplängel nur noch die Werte einsetzen:$$\tan(\varphi)= \sqrt{\frac{5^2+(-5)^2}{5}-1} = 3\\\vec n = \begin{pmatrix} 5\\-5 \end{pmatrix} \pm 3\cdot \begin{pmatrix} 5\\5 \end{pmatrix} \\ \vec n_1 = \begin{pmatrix} 20\\10 \end{pmatrix}\quad \vec n_2 = \begin{pmatrix} -10\\-20 \end{pmatrix}\\ t_1:\quad \vec n_1 \vec x = \vec n_1 S \implies 20x+10y=80 \implies 2x+y=8 \\ t_1:\quad \vec n_2 \vec x = \vec n_2 S \implies -10x -20y = -10 \implies x+2y=1$$Die Tangenten sind natürlich die selben wie oben, aber eben in der Koordinatenform dargestellt. Hier das Bild dazu
Melde Dich bitte, falls Du noch Fragen hast.
Gruß Werner
