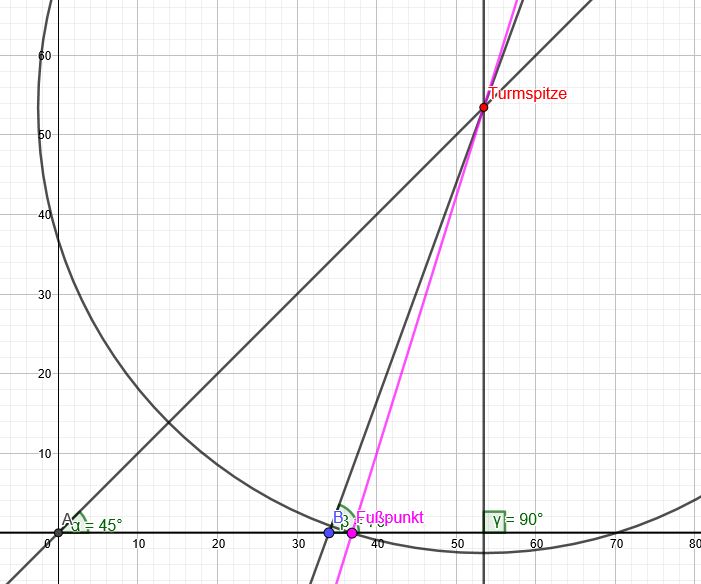
Ich wähle A\((0|0)\) und somit B\((34|0)\)
Gerade durch A mit \(m=\tan(45°)=1\):
\(y=x\)
Gerade durch B mit \(m=\tan(70°)\):
\( \frac{y}{x-34}=\tan(70°) \) →\(y=\tan(70°)x-34\cdot \tan(70°) \)
Schnitt beider Geraden:
\(\tan(70°)x-x =34\cdot \tan(70°) \)
\(x(\tan(70°)-1) =34\cdot \tan(70°) \)
Punkt C: \(x =\frac{34\cdot \tan(70°)}{\tan(70°)-1} \) \(y =\frac{34\cdot \tan(70°)}{\tan(70°)-1} \)
Kreis um C mit \(r=56\)
\((x-\frac{34\cdot \tan(70°)}{\tan(70°)-1})^2+(y-\frac{34\cdot \tan(70°)}{\tan(70°)-1})^2=56^2\)
Nullstelle ergibt den Fußpunkt des Turmes. (den Fußpunkt wählen, der Nachbar von B ist)
Über die Steigung der Geraden durch C und Fußpunkt lässt sich der Nebenwinkel des Neigungswinkels \( \varphi \) berechnen.
Die Summe vom Nebenwinkel und 90° und γ ist 180°.