Aufgabe:

Text erkannt:
\begin{tabular}{|ll}
\hline \( 7.000+20.000 \mathrm{VE}=10.000 \mathrm{VW} \) & \( 500 \mathrm{VW}=1.000 \mathrm{VE}+350 \) \\
\hline \( 9.550+500 \mathrm{VW}=100.000 \mathrm{VE} \) & \( 9.550+350+1.000 \mathrm{VE}=100.000 \mathrm{VE} \) \\
\hline & \( 9.900=99.000 \mathrm{VE} \) \\
& VE \( =\quad 0,1 € / \mathrm{kWh} \) \\
& \( 10.000 \mathrm{VW}=7.000+2.000 \) \\
& VW \( =\quad 0,9 € / \mathrm{cbm} \)
\end{tabular}
Problem/Ansatz:
Wie kam man hier auf VE = 0,1 und VW = 0,9??
Kann nicht nachvollziehen, wie aus
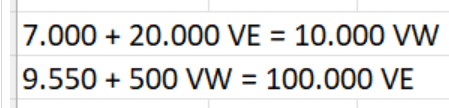
Text erkannt:
\( 7.000+20.000 \mathrm{VE}=10.000 \mathrm{VW} \)
\( 9.550+500 \mathrm{VW}=100.000 \mathrm{VE} \)
Das enstanden ist →

Text erkannt:
\( 500 \mathrm{VW}=1.000 \mathrm{VE}+350 \)
\( 9.550+350+1.000 \mathrm{VE}=100.000 \mathrm{VE} \)
\( 9.900=99.000 \mathrm{VE} \)