Gesetz von Cavalieri begründen?

Question

Hallo,

Ich bin bei einer Aufgabe etwas verwirrt.

Und zwar muss ich mit Hilfe des Prinzips von Cavalieri und den Strahlensätzen begründen, wieso Pyramiden mit flächengleichen Grundflächen und gleicher Höhe stets das Volumen besitzen.

Aber was kann man da noch begründen? Sie besitzen doch das gleiche Volumen, weil ihre Grundflache und Höhe gleich ist oder nicht.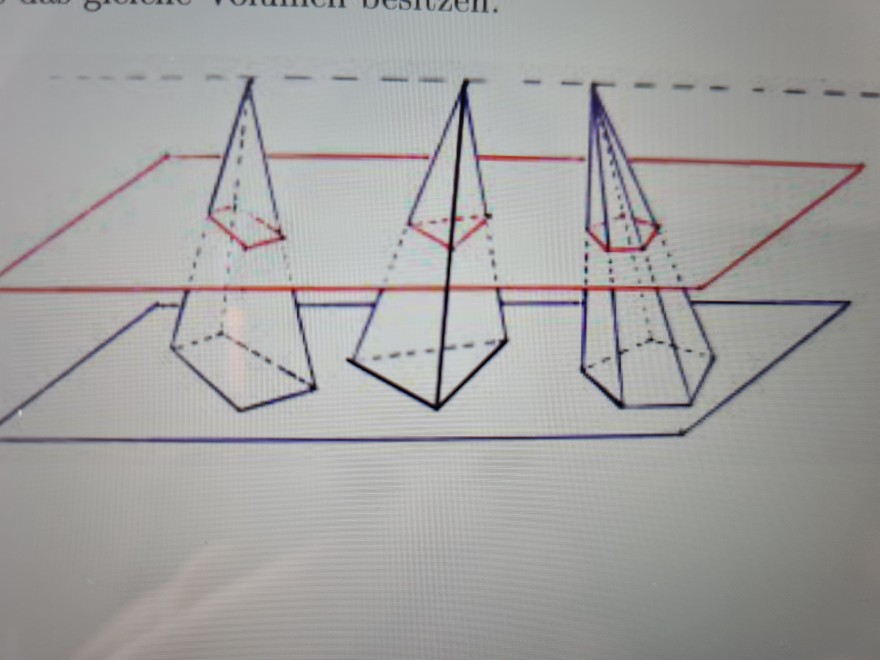

Vielen Dank für die Antworten!!!

Answer 1

Hallo

wegen des Strahlensatzes sind die entsprechenden Seitenlängen  in jeder Höhe gleich, damit auch die Flächen  A(h) in jeder Höhe und man kann die Pyramiden in dünne Scheiben  der Höhe dh schneiden  mit dem Volumen A(h)*dh (wie ein Haufen von Bierdeckeln gleicher Fläche)  und so das Volumen als Summe aller dieser dünnen Scheiben bestimmen.

Gruß lul  .