Guten Abend Werner,
vielen Dank nochmal. Bist du auch an "Beton" interessiert Formeln etc.?
Ich habe mich jetzt hingesetzt und das nach meiner Logik gelöst. Ich muss mir deine Lösung in Ruhe ansehen. Die Zeit hat mir heute leider gefehlt, da ich draußen etwas machen musste.
Ich habe das ganze mal in VBA getippt. Hier meine Lösung :o). Vielleicht gibts du mir eine Rückmeldung. Ich würde mich freuen.
Sub Dehnungsebene()
Dim alpha As Double, alpha_Tan As Double 'Nulllinienwinkel
Dim P0x As Double, P0y As Double, P0e As Double 'Koordinaten P1 und Dehnung an der Stelle e0
Dim P1x As Double, P1y As Double, P1e As Double 'Koordinaten P1 und Dehnung an der Stelle e1
Dim P2x As Double, P2y As Double, P2e As Double 'Koordinaten P2 und Dehnung an der Stelle e2
Dim P3x As Double, P3y As Double, P3e As Double 'Koordinaten P3 und Dehnung an der Stelle e3
Dim P4x As Double, P4y As Double, P4e As Double 'Koordinaten P1 und Dehnung an der Stelle e4
Dim pi As Double 'Herr PI
Dim m_G0 As Double, m_G1 As Double, m_G2 As Double 'Steigung der Geraden
Dim n_G0 As Double, n_G1 As Double, n_G2 As Double 'Schnittpunkt mit y-Achse
Dim kx As Double, ky As Double 'Verkrümmungen
Dim L23 As Double, L04 As Double 'Länge der Hilfsgeraden
pi = 4 * Atn(1)
Debug.Print "Ermittlung der Dehnungsebene:"
Debug.Print "-----------------------------"
Debug.Print ""
Debug.Print "Vorgabe von zwei Punkten und dem Winkel der Nulllinie"
Debug.Print "Definition: eps(x,y)= e0 + kx * x + ky * y"
P0x = 0
P0y = 0
P1x = -0.5
P1y = -0.85
P1e = -3
P2x = 0.4
P2y = 0.1
P2e = 4
alpha = -15
alpha_Tan = Tan(alpha * pi / 180)
Debug.Print "geg.:"
Debug.Print "P0x = " & P0x & " m"
Debug.Print "P0y = " & P0y & " m"
Debug.Print ""
Debug.Print "P1x = " & P1x & " m"
Debug.Print "P1y = " & P1y & " m"
Debug.Print ""
Debug.Print "P2x = " & P2x & " m"
Debug.Print "P2y = " & P2y & " m"
Debug.Print ""
Debug.Print "alpha = "; alpha; " °"
Debug.Print ""
Debug.Print "ges.:"
Debug.Print "Dehnungsebene: eps(x,y)= e0 + kx * x + ky * y"
m_G1 = alpha_Tan 'Steigung von f1(x)
m_G2 = -1 / m_G1 'Steigung von f2(x) - steht senkrecht auf f1(x)
m_G0 = m_G2
n_G0 = P0y - m_G0 * P0x
n_G1 = P1y - m_G1 * P1x
n_G2 = P2y - m_G2 * P2x
Debug.Print ""
Debug.Print "Lsg.:"
Debug.Print "Ermittle die Geradengleichung im Punkt P1 mit alpha = " & alpha & " °"
Debug.Print ""
If n_G1 >= 0 Then
Debug.Print "f1(x)= " & m_G1 & " * x + " & n_G1
Else
Debug.Print "f1(x)= " & m_G1 & " * x " & n_G1
End If
Debug.Print ""
Debug.Print "Ermittle die Geradengleichung im Punkt P2 senkrecht auf f1(x)"
Debug.Print ""
If n_G2 >= 0 Then
Debug.Print "f2(x)= " & m_G2 & " * x + " & n_G2
Else
Debug.Print "f2(x)= " & m_G2 & " * x " & n_G2
End If
Debug.Print ""
Debug.Print "Ermittle die Geradengleichung im Punkt P0 senkrecht auf f1(x)"
Debug.Print ""
If n_G0 >= 0 Then
Debug.Print "f3(x)= " & m_G0 & " * x + " & n_G0
Else
Debug.Print "f3(x)= " & m_G0 & " * x " & n_G0
End If
Debug.Print ""
'beide Funktionen gleichsetzen und nach x und y lösen
Debug.Print "Gleichungen f1(x) und f2(x) gleichsetzen, um den Schnittpunkt P3 zu bestimmen."
Debug.Print "Berechne den Hilfspunkt P3 - dieser liegt auf der verlängerten Linie von P1 und besitzt dieselbe Dehnung wie Punkt P1"
Debug.Print "Ausgabe der berechneten Koordinaten des Hilfspunktes P3:"
P3x = -(n_G1 - n_G2) / (m_G1 - m_G2)
P3y = (m_G1 * n_G2 - m_G2 * n_G1) / (m_G1 - m_G2)
Debug.Print "P3x = " & P3x & " m"
Debug.Print "P3y = " & P3y & " m"
Debug.Print ""
'beide Funktionen gleichsetzen und nach x und y lösen:
Debug.Print "Gleichungen f1(x) und f3(x) gleichsetzen, um den Schnittpunkt P4 zu bestimmen."
Debug.Print "Berechne den Hilfspunkt P4 - dieser liegt auf der verlängerten Linie von P1 und besitzt dieselbe Dehnung wie Punkt P1"
Debug.Print "Ausgabe der berechneten Koordinaten des Hilfspunktes P4"
P4x = -(n_G1 - n_G0) / (m_G1 - m_G0)
P4y = (m_G1 * n_G0 - m_G0 * n_G1) / (m_G1 - m_G0)
Debug.Print "P4x = " & P4x & " m"
Debug.Print "P4y = " & P4y & " m"
Debug.Print ""
Debug.Print "Berechne die Strecke zwischen P2 und P3"
'Länge Linie von P2 zu P3
L23 = Sqr((P3x - P2x) ^ 2 + (P3y - P2y) ^ 2)
Debug.Print "L23 = " & L23 & " m"
Debug.Print ""
Debug.Print "Berechne die Strecke zwischen P0 und P4"
'Länge Linie von P0 zu P4
L04 = Sqr((P0x - P4x) ^ 2 + (P0y - P4y) ^ 2)
Debug.Print "L04 = " & L04 & " m"
Debug.Print ""
Debug.Print "Bestimme die erste Unbekannte der Ebenengleichung - e0"
P0e = -(P1e * (L04 - L23) - P2e * L04) / L23
Debug.Print "P0e = " & P0e & " ‰ - Dehnung im Koordinatenursprung"
Debug.Print ""
Debug.Print "Berechne die Verkrümmungen kx und ky"
'berechne nun kx und ky - Auflösen von 2 Gleichungen mit zwei Unbekannten
kx = (P0e * (P1y - P2y) + P1e * P2y - P1y * P2e) / (P1x * P2y - P1y * P2x)
ky = -(P0e * (P1x - P2x) + P1e * P2x - P1x * P2e) / (P1x * P2y - P1y * P2x)
Debug.Print "kx = " & kx & " mm/m/m"
Debug.Print "ky = " & ky & " mm/m/m"
Debug.Print ""
Debug.Print "Dehungsebene:"
Debug.Print "eps(x,y)= " & P0e & " + " & kx & " * x + " & ky & " * y"
End Sub
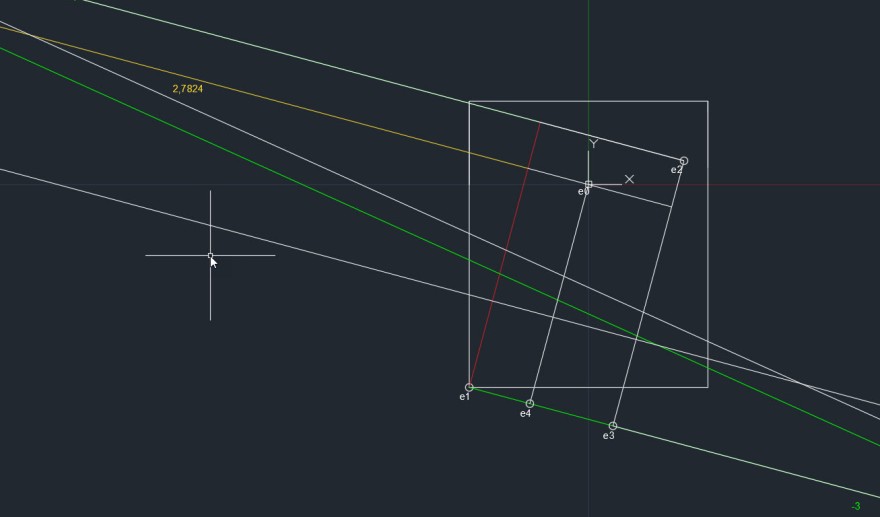
Und hier dazu die entsprechende Grafik.
Viele Grüße
Frank