Aloha :)
Ich denke, hier soll nicht einfach nur der Taschenrechner benutzt werden oder einfach nur die Cardanischen Formeln (zur exakten Lösung) verwendet werden, sondern hier soll ein konkretes Verfahren zur numerischen Nullstellenermittlung explizit angwendet werden.$$f(x)=4x^3-x^2-12x-3\stackrel!=0$$
Ein sehr gängiges Verfahren ist das Newton-Verfahren. Dabei startet man mit einem \(x\)-Wert \(x_0\) nahe einer vermuteten Nullstelle. Für diese Stelle \(x_0\) ermittelt man die Tangente an die Kurve. Diese hat die allgemeine Darstellung:$$t(x)=f(x_0)+f'(x_0)\cdot(x-x_0)$$Nun schaut man, an welcher Stelle diese Tangente die \(x\)-Achse schneidet. Man bestimmt also die Nullstelle der Tangente:$$0\stackrel!=t(x)=f(x_0)+f'(x_0)\cdot(x-x_0)\implies f'(x)\cdot(x-x_0)=-f(x_0)\implies$$$$x-x_0=-\frac{f(x_0)}{f'(x_0)}\implies x=x_0-\frac{f(x_0)}{f'(x_0)}$$Diese Nullstelle der Tangente verwendet man als neuen Näherungswert für die Nullstelle der Funktion und wiederholt das Verfahren.
Das führt zu folgender Rekursionsgleichung:$$\boxed{x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}}$$
Speziell für die Funktion \(f(x)\) in dieser Aufgabe lauetet die Ableitung:$$f'(x)=12x^2-2x-12$$sodass wir folgende Rekursionsgleichung erhalten:$$x_{n+1}=x_n-\frac{4x^3-x^2-12x-3}{12x^2-2x-12}$$
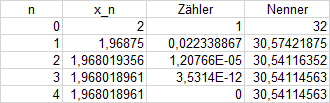
Für den Startwert \((x_0=2)\) erhalten wir die Nullstelle: \(x_0\to1,968\)
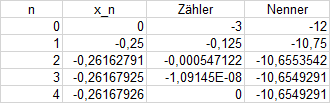
Für den Startwert \((x_0=0)\) erhalten wir die Nullstelle: \(x_0\to-0,262\)
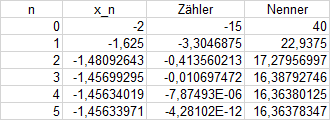
Für den Startwert \((x_0=-2)\) erhalten wir die Nullstelle: \(x_0\to-1,456\)