1)
a) M ist der Umkreismittelpunkt und liegt auf AB
Daraus folgt, dass AB der Durchmesser des Umkreises sein muss und dass M somit Mittelpunkt von AB ist.
Zeichne also einen Kreis, markiere seinen Mittelpunkt und bezeichne diesen mit M. Zeichne dann eine (horizontale) Gerade durch M und bezeichne den linken Schnittpunkt dieser Geraden mit dem Kreisrand mit A bzw. den rechten mit B.
b) AB und CM stehen senkrecht aufeinander
Daraus und aus a) folgt, dass CM Mittelsenkrechte zu AB ist.
Konstruiere also die Mittelsenkrechte zur Strecke AB und bezeichne den oberhalb der Geraden AB liegenden Schnittpunkt der Mittelsenkrechten mit dem Kreisrand mit C.
c) der Punkt D liegt auf den Umkreis auf den Bogen zwischen A und C so dass der Winkel MDB 15° ist.
Da sowohl MD als auch MB Radien des Umkreises sind, ist das Dreieck MDB gleichschenklig. Dann aber gilt: Wenn der Winkel MDB 15 ° ist, dann ist auch der Winkel MBD 15 ° . Der Winkel MBD = 15 ° aber lässt sich leicht konstruieren und damit lässt sich auch der Punkt D leicht finden.
Zeichne also in Punkt B eine Gerade ein, so dass der Winkel zwischen dieser Geraden und der Strecke MB 15 ° ist. Bezeichne den zweiten Schnittpunkt dieser Geraden mit dem Kreisrand mit D.
d) Punkt P liegt auf CM so dass PD ist parallel zu AB
Zeichne also eine Parallele zu AB durch den Punkt D. Der Schnittpunkt dieser Parallelen mit der Strecke CM ist der Punkt P.
So sollte das Ganze dann etwa aussehen:
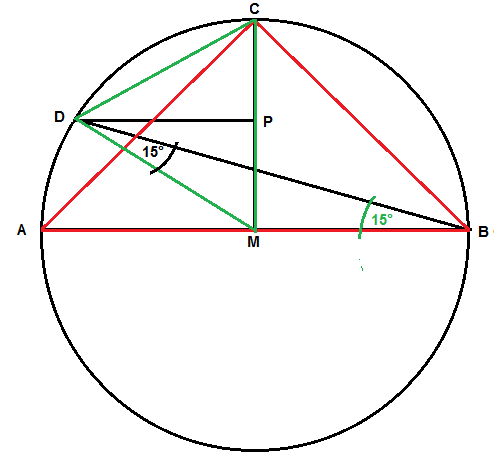
In Rot eingezeichnet ist das Dreieck ABC, welches in der Aufgabenstellung beschrieben ist.
2)
In Grün ist das Dreieck MCD eingezeichnet, von dem gezeigt werden soll, dass es gleichseitig ist. Dazu zeigt man zunächst, dass der Winkel DMC 60 ° groß ist. Betrachte dazu das Dreieck DMB. Es handelt sich um ein gleichschenkliges Dreieck, dessen Basiswinkel jeweils 15 ° groß sind. Folglich hat der Scheitelwinkel DMB dieses Dreiecks die Größe
180 ° - 2 * 15 ° = 150 °
Da aber der Winkel CMB ein rechter Winkel ist, muss für den Winkel CMD gelten:
CMD = 150 ° - 90 ° = 60 °
Mit dieser Winkelgröße und den Schenkeln CM und DM dieses Winkels, die beide Radien des Kreises sind und daher beide die Länge r haben, kann man mit Hilfe des Kosinussatzes die Länge der Strecke CD berechnen:
CD 2 = r 2 + r 2 - 2 * r * r * cos ( 60 ° )
= 2 r 2 - 2 r 2 * 0,5
= r 2
<=> CD = r
Also sind alle 3 Seiten des grün eingezeichneten Rechtecks gleich lang (Länge r) und damit handelt es sich um ein gleichseitiges Dreieck.
3)
Der Winkel BDP ist Wechselwinkel des Winkels MBD und hat daher die gleiche Größe wie dieser, nämlich 15 ° Zusammen mit dem Winkel MDB (ebenfalls 15 °) bildet er den Winkel MDP, der also 30 ° groß ist. Daher ist die Strecke DP Winkelhalbierende des Winkels MDC, der als Winkel eines gleichseitigen Dreiecks die Größe 60° hat.
Da das Dreieck MCD, wie gezeigt, gleichseitig ist, ist jede seiner Winkelhalbierenden gleichzeitig auch Seitenhalbierende der gegenüberliegenden Seite. Daher ist insbesondere auch die Winkelhalbierende DP gleichzeitig Seitenhalbierende der Seite MC. Da MC Radius des Kreises ist und also die Länge r hat, hat die Strecke PC daher die Länge r / 2
Die Strecke AB wiederum ist Durchmesser des Kreises und hat daher die Länge 2 r
Es gilt also:
PC / AB = ( r / 2 ) / ( 2 r )
= r / ( 4 r )
= 1 / 4
<=> PC = AB / 4