Question

Bestimme die allgemeine Lösung der folgenden Bernoulli’schen Differentialgleichung

(1+x²)y′ +xy−xy² =0,

u = y⁻¹ − 1

danke im voraus

Answer 1

Hallo,

Die DGL kann auch via Trennung der Variablen gelöst werden, aber so lautete die Aufgabe wohl nicht, denke.

meine Berechnung:

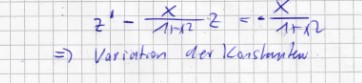
z' - ( x/(1+x^2) z = 0 ->via Trennung der Variablen

dz/z= (x/(1+x^2)) dx

zh= C1 √(x^2+1) ;Setze C1= C(x)

zp= C(x) √(x^2+1)

zp'= C'(x) √(x^2+1)+ (C(x) *x)/(√x^2+1)

--->

zp und zp' in die DGL mit z einsetzen:

C(x) hebt sich auf---->

C(x)= 1/√(x^2+1)

----------->

zp= C(x) √(x^2+1) = 1

z=zh+zp

z= C√(x^2+1)+1

Resubstitution z=1/y

y= 1/(C √x^2+1) +1) ->Lösung