Aufgabe
Problem/Ansatz:
Text erkannt:
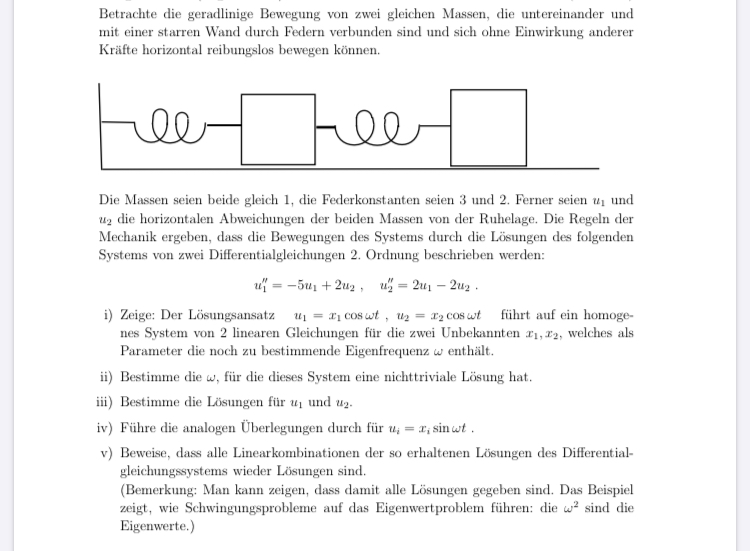
Betrachte die geradlinige Bewegung von zwei gleichen Massen, die untereinander und mit einer starren Wand durch Federn verbunden sind und sich ohne Einwirkung anderer Kräfte horizontal reibungslos bewegen können.
Die Massen seien beide gleich 1, die Federkonstanten seien 3 und 2 . Ferner seien \( u_{1} \) und \( u_{2} \) die horizontalen Abweichungen der beiden Massen von der Ruhelage. Die Regeln der Mechanik ergeben, dass die Bewegungen des Systems durch die Lösungen des folgenden Systems von zwei Differentialgleichungen 2. Ordnung beschrieben werden:
\( u_{1}^{\prime \prime}=-5 u_{1}+2 u_{2}, \quad u_{2}^{\prime \prime}=2 u_{1}-2 u_{2} . \)
i) Zeige: Der Lösungsansatz \( u_{1}=x_{1} \cos \omega t, u_{2}=x_{2} \cos \omega t \) fihrt auf ein homogenes System von 2 linearen Gleichungen für die zwei Unbekannten \( x_{1}, x_{2} \), welches als Parameter die noch zu bestimmende Eigenfrequenz \( \omega \) enthält.
ii) Bestimme die \( \omega \), für die dieses System eine nichttriviale Lösung hat.
iii) Bestimme die Lösungen für \( u_{1} \) und \( u_{2} \).
iv) Führe die analogen Überlegungen durch für \( u_{i}=x_{i} \sin \omega t \).
v) Beweise, dass alle Linearkombinationen der so erhaltenen Lösungen des Differentialgleichungssystems wieder Lösungen sind.
(Bemerkung: Man kann zeigen, dass damit alle Lösungen gegeben sind. Das Beispiel zeigt, wie Schwingungsprobleme auf das Eigenwertproblem führen: die \( \omega^{2} \) sind die Eigenwerte.)
Kann mir da jemand helfen?
Bin ziemlich überfordert mit der Aufgabe...