Doppelintegrale lösen im R^2

Question

Aufgabe:

\( \int \limits_{0}^{1} \int \limits_{0}^{2} e^{\frac{x}{y}} d y d x=\int \limits_{0}^{1}\left[-\frac{1 x^{2}}{x} e^{\frac{x}{y}}\right]_{2 x}^{2} d x=\int \limits_{0}^{1}-\frac{4}{x} e^{\frac{x}{2}}+\frac{x^{2}}{x} e^{\frac{x}{x}} d x=\int \limits_{0}^{1}-\frac{4}{x} e^{\frac{x}{2}}+4 x e^{\frac{1}{2}} d x=\left[+2 E x^{2}\right]_{0}^{1} \)

\( \int \limits_{0}^{1} \int \limits_{1}^{1} \sqrt[3]{\sqrt{3^{3}+4}} \cdot d y d x=\int \limits_{0}^{1}[ \)

Ich habe versucht diese Integrale zu lösen, und scheitere bei den Stammfunktionen. Ich habe diese auch in einen Onlinerechner schon eingegegben, aber dort konnte mir auch nicht geholfen werden (beim zweiten integral wurde nichtmal eine Stammfunktion gefunden). Gibt es Tipps wie ich diese lösen kann?

Und ist das obere Integral denn bis dahin richtig gelöst?

Answer 1

Aloha :)

$$I=\int\limits_{x=0}^1\;\;\int\limits_{y=2x}^2e^{-\frac xy}\,dx\,dy=\cdots$$Da das Integral über \(dy\) einen Ausdruck ergibt, der umständlich nach \(dx\) zu integrieren ist, würde ich hier die Integrationsintervalle ersetzen. Aktuell haben wir:$$0\le x\le1\quad;\quad 2x\le y\le2$$Das ist ein Dreieck

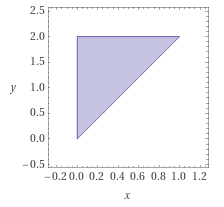
und kann ebenso wie folgt parametrisiert werden:$$0\le y\le 2\quad;\quad 0\le x\le\frac y2$$

Damit kölnnen wir das gesuchte Integral umschreiben:$$I=\int\limits_{y=0}^2\;\int\limits_{x=0}^{y/2}e^{-\frac xy}\,dx\,dy=\int\limits_{y=0}^2\left[-ye^{-\frac xy}\right]_{x=0}^{y/2}dy=\int\limits_0^2\left(-ye^{-\frac12}+ye^0\right)\,dy$$$$\phantom{I}=\int\limits_0^2\left(1-\frac{1}{\sqrt e}\right)y\,dx=\left(1-\frac{1}{\sqrt e}\right)\left[\frac{y^2}{2}\right]_0^2=2\left(1-\frac{1}{\sqrt e}\right)$$