Berechne den Flächeninhalt der rot straffierten Fläche.

Question

Aufgabe:

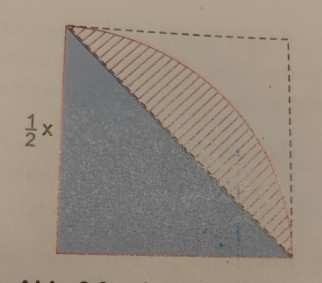
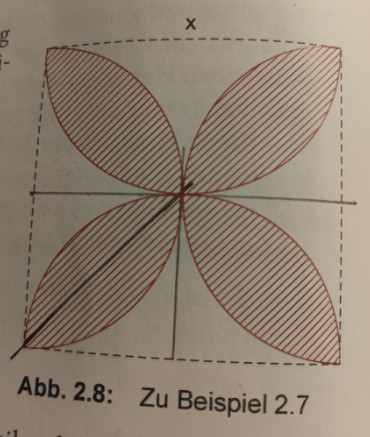
Berechne den Flächeninhalt der rot straffierten Fläche.

Hallo! Ich habe kein Problem mit dem Lösungsansatz und brauche auch keine Lösung da die schon im Heft steht. Mich würde interessieren wie man auf den Annahme kommt, dass die abgebildete straffierte Fläche ein Viertelkreis ist (im 2. Bild mit dem blauen Dreieck). Würde die straffierte Fläche bis nach unten links ins blaue Dreieck gehen, würde ich den Viertelkreis eindeutig erkennen können.

Answer 1

Der Viertelkreis ist rot umrandet und nicht rot schraffiert. Wichtig ist zunächst den Text richtig zu lesen. Das rot schraffierte ist die Differenz.

Comments

Abend! :)

Ja das hatte ich auch schon in betracht gezogen, aber das wär dann ja nicht mehr die Figur die in der Aufgabe abgebildet ist. Laut der Skizze mit dem blauen Dreieck, müsste dieser Kreis (wenn die durchgezogene rote Linie für das Viertel steht), ja bis unten links ins Eck gehen, dann wäre es ein ganzer Viertelkreis für mich. Aber das tut sie ja nicht.

---

Das wäre ein Viertelkreis für mich. Aber so ist die Blüte ja nicht auf das Viertel vom Quadrat aufgeteilt.

---

Suche die rote durchgezogene Linie

Ergibt die Figur mit der roten durchgezogenen Linie einen Viertelkreis?

Ist es nur klar, wie du daraus die schraffierte Fläche berechnest?

---

Text erkannt:

Abb. 2.8: Zu Beispiel \( 2.7 \)

Ja, das ist ein Viertelkreis für mich (nochmal rot umrandet). Aber der entspricht ja nicht der tatsächlichen Abbildung. In der eigentlichen Abbildung geht der Viertelkreis nicht nach unten links in Eck, sondern dort ist auch nochmal eine freie Fläche (hier in Gelb)

---

Viertelkreis (rot umrandet) - Dreieck (blau) = Halbes Blütenblatt (schraffiert)

8 Halbe Blütenblätter (schraffiert) = 1 Blume

---

Achso. Ja ich hatte einen kompletten Denkfehler. Jetzt habe ichs verstanden. Vielen Dank! Manchmal hackts bei mir ,)

Answer 2

Hallo,

du musst nur die Kreislinie betrachten, nicht die schraffierte Fläche, um den Viertelkreis zu erkennen.

Ich finde, dass in der dritten Abbildung die Halbkreise noch besser zu erkennen sind.

:-)

Comments

Ja den hatte ich direkt erkannt. Nur ich dachte der Autor vom Buch meint das nur die straffierte Fläche ein Viertelkreis wäre. Mir ist komplett entgangen das er nur meinte, Viertelkreis minus blaues Dreieck ist die straffierte Fläche. Aber danke für die Antwort :)