Kurvenintergral, weg unabhängigkeit

Question

Gegeben sei die Kurve \( \gamma:[0, \ln 2] \rightarrow \mathbb{R}^{3} \) mit \( \gamma(t)=(\sinh (t), \cosh (t), \sinh (t))^{\top} \) sowie das Vektorfeld \( v: \mathbb{R}^{3} \rightarrow \mathbb{R}^{3} \) mit \( v(x, y, z)=(y,-z, x)^{\top} \).
a) Berechnen Sie

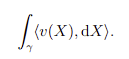
Text erkannt:

\( \int \limits_{\gamma}\langle v(X), \mathrm{d} X\rangle \)

b) Ist dieses Kurvenintegral bei dem gegebenen Vektorfeld \( v \) wegunabhängig? Begründen Sie Ihre Antwort.

Kann jemand diese Aufgabe vorrechnen?

Answer 1

Aloha :)

zu a) Das Kurvenintegral kannst du direkt formulieren:$$E=\int\limits_{\gamma}\vec v\,d\vec r=\int\limits_{0}^{\ln(2)}\vec v\,\frac{d\vec r}{dt}\,dt=\int\limits_{0}^{\ln(2)}\begin{pmatrix}y=\cosh(t)\\-z=-\sinh(t)\\x=\sinh(t)\end{pmatrix}\,\begin{pmatrix}\cosh(t)\\\sinh(t)\\\cosh(t)\end{pmatrix}\,dt$$$$\phantom E=\int\limits_0^{\ln(2)}\left(\underbrace{\cosh^2(t)-\sinh^2(t)}_{=1}+\sinh(t)\cosh(t)\right)\,dt=\left[t+\frac12\sinh^2(t)\right]_0^{\ln(2)}$$$$\phantom E=\ln(2)+\frac12\left(\frac34\right)^2=\ln(2)+\frac{9}{32}$$

zu b) Wir betrachten die Rotation des Vektorfeldes \(\vec v\):$$\operatorname{rot}\vec v=\begin{pmatrix}\partial_x\\\partial_y\\\partial_z\end{pmatrix}\times\begin{pmatrix}y\\-z\\x\end{pmatrix}=\begin{pmatrix}0+1\\0-1\\0-1\end{pmatrix}=\begin{pmatrix}1\\-1\\-1\end{pmatrix}\ne\vec 0$$Da die Rotation des Vektorfeldes \(\vec v\) nicht verschwindet, ist die Integrabilitätsbedingung verletzt, sodass es keine Funktion \(\phi(x;y;z)\) geben kann mit \(\vec v=\operatorname{grad}\phi\). Daher ist das Kurvenintegral durch das Vektorfeld \(\vec v\) abhängig vom gewählten Weg.