Ich hab letztes Jahr mit meinem Statistik Seminar eine Befragung durchgeführt und bei der Auswertung sind wir auf folgendes Phänomen gestoßen. Wir haben bei der Zusammenhangsanalyse korrigierte Kontingenzkoeffizienten berechnet - jeweils mit unklassierten und dann auch nochmal mit klassierten Daten. Dabei ist uns aufgefallen, dass die korrigierten Kontingenzkoeffizienten der klassierten Daten immer niedriger ausfallen, als die Koeffizienten bei den jeweils dazugehörigen unklassierten Daten. Meine Fragen:
1. Ist das IMMER so?
2. Wie kommt es dazu? Ich meine die Grundwerte der Berechnung sind ja immer gleich, sie werden dann eben nur in die Klassen zusammenaddiert.
Danke für die Antworten im Voraus!
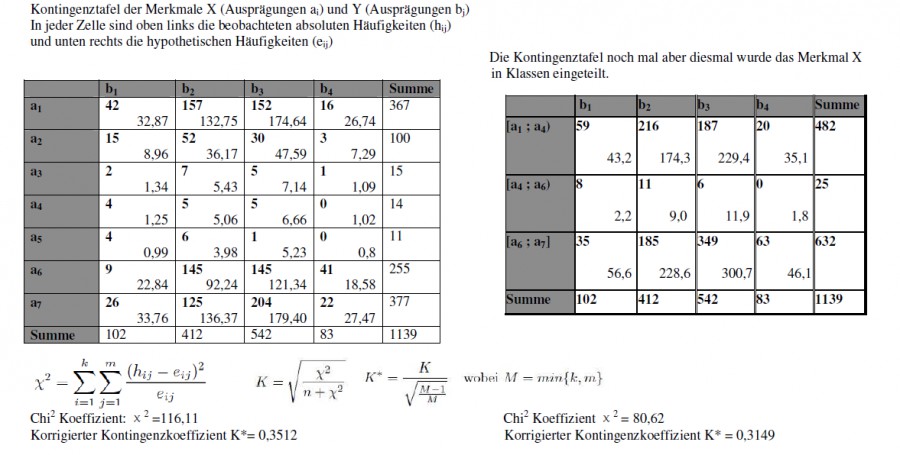
PS: Hier noch ein Beispiel für eine unserer Kontingenztafeln: