Text erkannt:
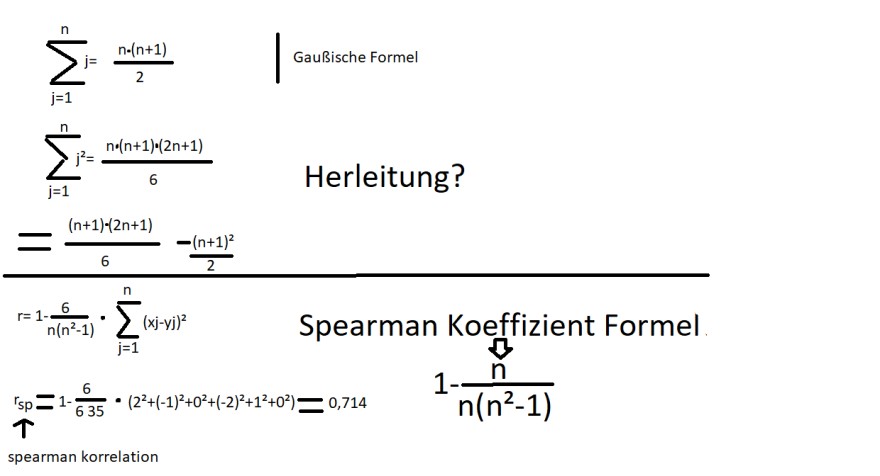
\( \begin{array}{l}\sum \limits_{j=1}^{n}=\frac{n \cdot(n+1)}{2} \\ \sum \limits_{j=1}^{n}=\frac{n \cdot(n+1)(2 n+1)}{6} \\ \text { Herleitung? } \\ =\frac{(n+1)(2 n+1)}{6}-\frac{(n+1)^{2}}{2} \\ \left.=1=\frac{6}{n\left(n^{2}-1\right)} \cdot \sum \limits_{j=1}^{n}(x)-j\right)^{2} \quad \text { Spearman Koeffizient Formel } \\ \mathrm{rsp}_{\mathrm{sp}}=1 \cdot \frac{6}{635} \cdot\left(2^{2}+(-1)^{2}+0^{2}+(-2)^{2}+1^{2}+0^{2}\right)=0,714 \quad 1-\frac{n}{n\left(n^{2}-1\right)} \\\end{array} \)
Problem/Ansatz:
Ich würde gerne wissen wie die Gaußische Formel und die Spearman Koeffizient Formel zusammenhängen. In der Abbildung wird die Gaußische Formel verwendet, ist das einfach nur eine Herleitung, wie sich die Spearman Formel ergibt, oder hat die gaußische Formel in dieser Abbildung eine tiefere Bedeutung?
Ich bearbeite gerade paar Aufgaben, wo man die Spearman Formel benötigt. Daher die Frage, ob ich die Gaußische Formel ignorieren kann, falls sie nur den Aufbau der Herleitung darstellt und ich mich auf die Spearman Formel konzentrieren kann, die ich mit einem Pfeil markiert hab